Radio/TV Broadcasting and the Tuning Circuit

Broadcasting and Frequency Allocation

The AM radio frequency range is from 535 kHz to 1605 kHz with 10 kHz frequency spacing or bandwidth, i.e., the highest signal frequency allowed is about 5 kHz (while the upper limit of the audible frequencies is 20 kHz).
The FM radio frequency range (VHF) is from 88 MHz to 108 MHz with 0.2 MHz=200 kHz frequency spacing, corresponding to a much wider bandwidth that makes high fidelity and stereo broadcasting possible.
The TV broadcasting is also in MHz frequency range with a much wider spacing of 6 MHz, needed to carry video as well as audio signals.
- VHF: 54 MHz to 210 MHz (not continuous, for channels 2 to 13)
- UHF: 470 MHz to 884 MHz (not continuous, for channels 14 to 83)

The Federal Communications Commission (FCC) has very specific frequency allocation regulations, see the FCC frequency allocation chart.

Example 1:

Resonant circuit is widely used in radio and TV receivers to select a desired station from many stations available. The tuning circuit shown in the figure below is a series RCL circuit composed of an inductor $L$ , a resistor $R$ (of the inductor) and variable capacitor $C$ , which is adjustable to match the resonant frequency of the circuit to the frequency of the desired radio station. The voltage across $C$ is to be amplified by the subsequent circuits.

If $L=80\mu H$ , $R=8\Omega$ , find the value of $C$ for this circuit to resonate at $f=400\;kHz$ , also find the bandwidth.

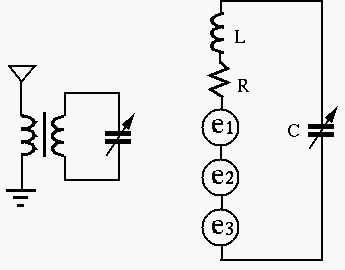
Solution:

$\displaystyle \omega_n=\frac{1}{\sqrt{LC}},\;\;\;\; C=\frac{1}{\omega_n^2 L}=\frac{1}{(2\pi 400\times 10^3)^2\times 80\times 10^{-6}} =20nF$

(366)

The quality factor is

$\displaystyle Q=\frac{\omega_n L}{R}=\frac{2\pi 400\times 10^3\times 80\times 10^{-6}}{8}=25.13$

(367)

The bandwidth is

$\displaystyle \triangle f=\frac{f_0}{Q}=\frac{400\times 10^3}{25.13}=15.9\;kHz$

(368)

$\displaystyle \triangle \omega= 2\pi\triangle f=\frac{\omega_n}{Q}=\frac{R}{L}=10^5$

(369)

Example 2:

Assume $L=0.3\; mH,\;\;R=16\;\Omega$ , and the frequency of the desired station is 640 kHz, find the value of $C$ and the bandwidth of the tuning circuit. Moreover, if the induced voltage in the circuit is $e=2\;\mu V$ (rms), find the current (rms) in the resonant circuit, and the output voltage (rms) across the capacitor.

Solution: At the desired resonant frequency $f=640\;kHz$ , the reactance of the inductor is

$\displaystyle X_L=\omega L=2\pi f L =2\times 3.14\times 640\times 10^3\times 0.3\times 10^{-3}=1206\;\Omega$

(370)

and the quality factor $Q$

of this circuit is

$\displaystyle Q=\frac{X_L}{R}=\frac{\omega L}{R}=\frac{1206}{16}\approx 75$

(371)

The bandwidth is:

$\displaystyle \triangle f =\frac{f_0}{Q}=\frac{640}{75}\approx 8.53\;kHz$

(372)

The resonant frequency can be expressed as:

$\displaystyle f_0=\frac{\omega_0}{2\pi}=\frac{1}{2\pi\sqrt{LC}}=640\;kHz$

(373)

Solving this we get

$\displaystyle C=\frac{1}{(2\pi f_0)^2L}=206\times 10^{-12}F=206\;pF$

(374)

The current in circuit is

$\displaystyle I_{rms}=e/R=2\times 10^{-6}/16=0.125\times 10^{-6}\; A =0.125\;\mu A$

(375)

The voltage across $R$

$\displaystyle V_R=I_{rms} R=0.125\times 16\times 10^{-6}=2\times 10^{-6}\;V=0.002\;mV$

(376)

The output voltage across $C$

$\displaystyle V_C = V_L=I_{rms} X_L=0.125\times 10^{-6}\times 1206=150\times 10^{-6}\;V =150\;\mu V =0.150\;mV=Q\,V_R$

(377)

which is

times the voltage $V_R=2\times 10^{-6}$ across $R$

(same as the voltage source).

Example

In reality, all inductors have a non-zero resistance, therefore a parallel resonance circuit should be modeled as shown in the figure.

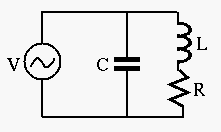
The admittance is:

$\displaystyle Y(\omega)$	$\displaystyle =$	$\displaystyle \frac{1}{R+j\omega L}+j\omega C =\frac{R-j\omega L+j\omega C(R^2+\omega^2L^2)}{R^2+\omega^2L^2}$
	$\displaystyle =$	$\displaystyle \frac{1}{R^2+\omega^2L^2}[R-j(\omega L-\omega C(R^2+\omega^2L^2))]$	(378)

As frequency $\omega$ appears in the real part $Re[Y(\omega)]$ as well as in the imaginary part $Im[Y(\omega)]$ , the frequency that minimizes $\vert Y(\omega)\vert$ has to be found by solving

$\displaystyle \frac{d}{d\omega} \; \vert Y(\omega)\vert =0$

(379)

However, when the quality factor $Q=\omega_n L/R$ associated with the non-ideal inductor is large enough (e.g., $Q > 20$

), all previous discussed relations for ideal inductors still hold approximately, and the resonant frequency $\omega_n$ can still be found approximately by the previous approach by letting $Im[Y(\omega)]=0$ :

$\displaystyle \omega_n L=\omega_n C(R^2+\omega_n^2L^2),\;\;\;\;\Longrightarrow \;\;\;\;\;\omega_n=\sqrt{\frac{1}{LC}-\left(\frac{R}{L}\right)^2}$

(380)

For $\omega_n$ to be real, we must have

$\displaystyle \frac{1}{LC} > (\frac{R}{L})^2, \;\;\;\;\;\;$ i,e, $\displaystyle \;\;\;\;\;\;R<\sqrt{\frac{L}{C}}$

(381)

Typically we have $R \ll \sqrt{L/C}$ , and the resonant frequency is

$\displaystyle \omega_n=\sqrt{\frac{1}{LC}-\left(\frac{R}{L}\right)^2}\approx \frac{1}{\sqrt{LC}}$

(382)

Note: For the same reason, when considering the transfer function of a series RCL circuit when the output is the voltage across either $C$ or $L$ , the peak frequency $\omega_p$ is not exactly the same as the resonant frequency $\omega_n$ , which only minimizes the denominator, but the numerator is still a function of $\omega$ . Only when the output is the voltage across $R$ (i.e., the numerator is $R$ , a constant, not a function of $\omega$ ), will the resonant frequency $\omega_n$ be the same as the peak frequency.

Amplitude, Phase, and Frequency Modulations

In radio or TV broadcast, the audio or video signal $s(t)$ to be transmitted is used to modulate the amplitude, phase, or frequency of the carrier signal $c(t)=\cos(\omega_c t)$ with carrier frequency $\omega_c=2\pi f_C$ , which is much higher than the highest frequency component of the signal $s(t)$ . The modulated signal $x(t)$ is then transmitted.

Amplitude Modulation (AM)
The amplitude of the carrier is modulated by the signal and becomes time variant:

$\displaystyle x(t)=\cos(\omega_c t)\,[1+k_a s(t)]$ (383)

where is the amplitude modulation index, and we assume the amplitude of the signal is no greater than 1. For example, if the signal is sinusoidal $s(t)=\cos(\omega_s t)$ and , then the modulated signal is:

$\displaystyle x(t)=\cos(\omega_ct)[1+\cos(\omega_st)] =\cos(\omega_ct)+\frac{1}{2}[\cos(\omega_c+\omega_s)t+\cos(\omega_c-\omega_s)t]$ (384)

In order to transmit all signal frequencies up to the highest frequency component $\omega_{max}$ in the signal, a bandwidth of $\triangle\omega=(\omega_c+\omega_{max})-(\omega_c-\omega_{max})=2\omega_{max}$ centered around the carrier (or central) frequency $\omega_c$ is required.
Phase Modulation (PM)
The phase of the carrier is modulated by the signal and becomes time variant:

$\displaystyle x(t)=\cos(\omega_ct+k_p s(t))$ (385)

where is the phase modulation index. For example, if the signal is sinusoidal $s(t)=\cos(\omega_s t)$ , then the modulated signal is:

$\displaystyle x(t)=\cos(\omega_ct+k_p \cos(\omega_st))$ (386)

where is the phase modulation index. The phase angle of the carrier is modulated to vary within the range of $(-k_p,\;k_p)$ .
Frequency Modulation (FM)
The frequency of the carrier is modulated by the signal and becomes time variant:

$\displaystyle \omega(t)=\omega_c+k_f s(t)$ (387)

where is the frequency modulation index. As $\omega(t) =d\phi(t)/dt$ , the angle is also time variant:

$\displaystyle \phi(t)=\int_0^t\omega(\tau)d\tau=\int_0^t ( \omega_c+k_f s(\tau)) d\tau =\omega_c t+k_f \int_0^t s(\tau)d\tau$ (388)

and the modulated signal is:

$\displaystyle x(t)=\cos(\phi(t))=\cos\left(\omega_c t+k_f \int_0^t s(\tau)d\tau\right)$ (389)

For example, if the signal is sinusoidal $s(t)=\cos(\omega_s t)$ , then the modulated signal is:

$\displaystyle x(t)=\cos\left(\omega_c t+k_f \int_0^t \cos(\omega_s \tau)d\tau\right) =\cos\left(\omega_c t+\frac{k_f}{\omega_s} \sin(\omega_s t)\right)$ (390)

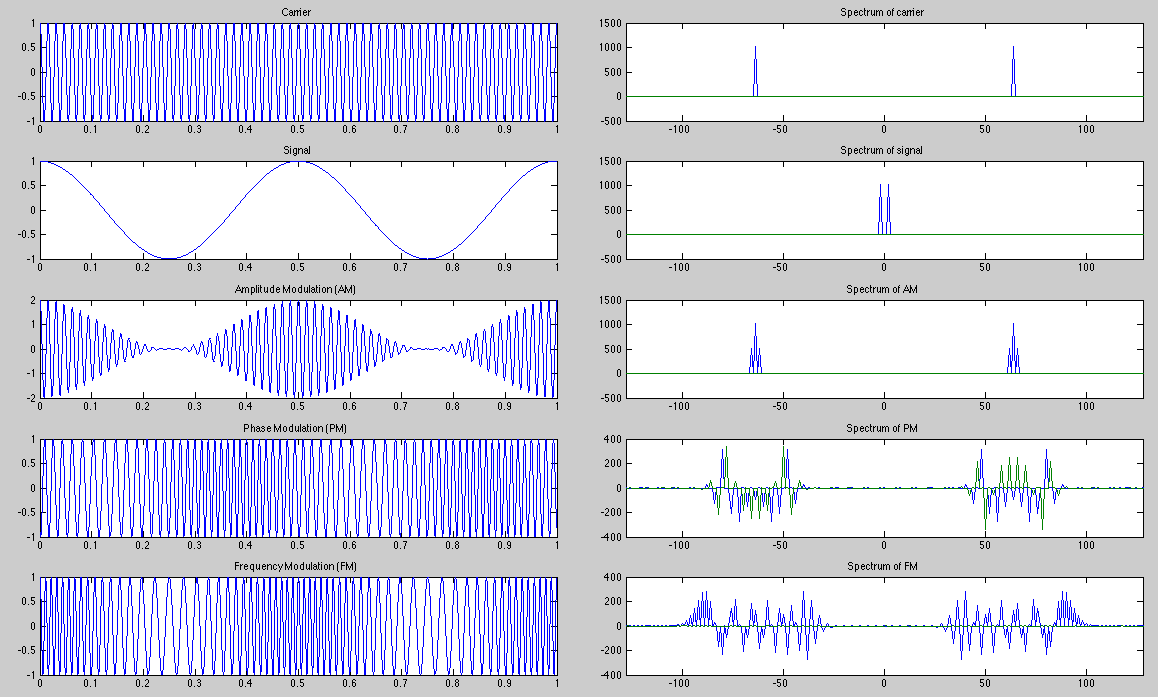
The amplitude-modulated signal can be demodulated to recovered the signal $s(t)$ from the transmitted signal by RF amplification, rectification, low-pass filtering, and audio signal amplification.

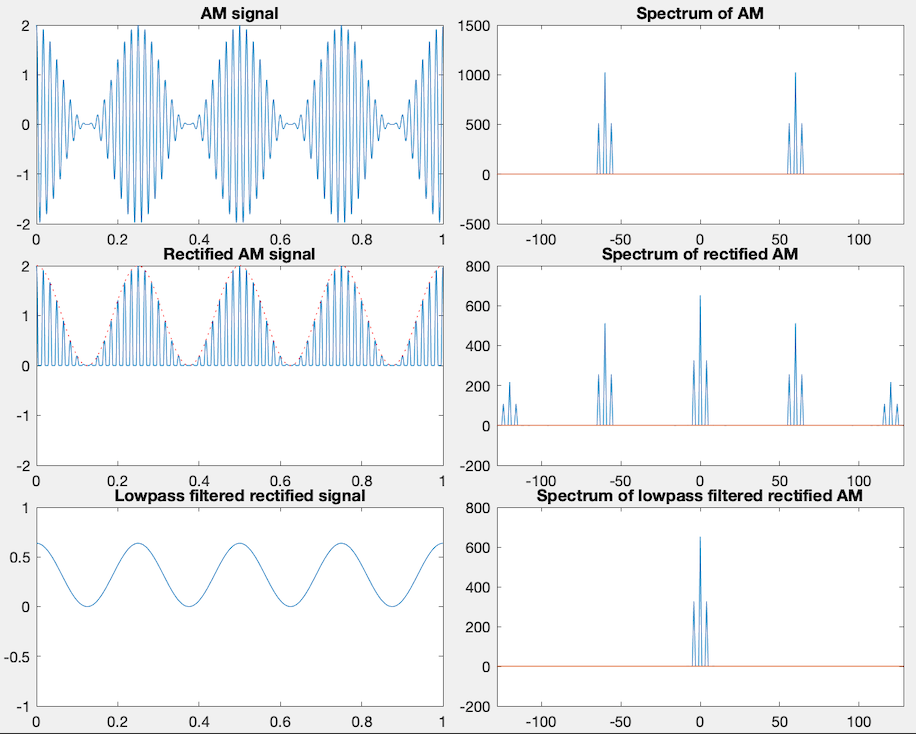
In any of the three case above, it requires a certain bandwidth around the carrier frequency $\omega_c$ to transmit the modulated signal. Consequently, the $Q$ value of the tuner of the receiver needs to be very carefully chosen. It needs to be high enough for good selectivity between different radio stations, but, on the other hand, it cannot be too high in order to have a bandwidth wide enough to contain all frequency components in the signal.

In digital broadcasting, the information to be broadcast is first converted into digital signal, which is then used to modulate the phase, amplitude or frequency of the carrier signal at certain radio frequency: