Next: Two-Port Networks Up: Chapter 2: Circuit Principles Previous: Solving Circuits with Kirchoff
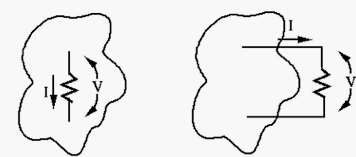
A generic system with input (stimulus, cause) 


 |
(19) |
 |
(20) |
 |
(21) |
 , we can consider several causes (e.g.,
, we can consider several causes (e.g.,  and
and  ) individually and then combine the individual responses (
) individually and then combine the individual responses ( and
and  ). An electrical system of linear components (with linear
voltage-current relation) is a linear system (if only voltage and current
are of interest). When the circuit is linear, the following applies:
). An electrical system of linear components (with linear
voltage-current relation) is a linear system (if only voltage and current
are of interest). When the circuit is linear, the following applies:
Superposition Principle:
When there exist multiple energy sources in the circuit, any voltage and current in the circuit can be found as the algebraic sum of the corresponding values obtained by assuming only one source at a time, with all other sources turned off:
As superposition principle only applies to linear functions, it cannot be
applied to nonlinear functions such as power (e.g., 

 |
(22) |
 (
( short-circuit) and
short-circuit) and  (
( short-circuit).
short-circuit).
 |
(23) |
 (
( open circuit) and
open circuit) and  (
( open circuit).
open circuit).
However, note that superposition principle does not apply to any variable nonlinearly related to the energy sources, such as power:
 |
(24) |
Example 1: The previous example can also be solved by superposition theorem.
First, we turn the voltage source of 20V off (short-circuit with 0V), and get
 |
(25) |
 |
(26) |
 |
(27) |
Example 2: Find the voltage across the parallel combination
of two branches




This problem can be solved by different methods:
 |
(28) |
 and
and  are
are
 |
(29) |
 .
.
 |
(30) |
 , and the total resistance is
, and the total resistance is
 . This current source can be
converted into a voltage source with
. This current source can be
converted into a voltage source with  and
and
 .
In either case, we get the voltage
.
In either case, we get the voltage
 .
.
 and
and  alone:
alone:
 |
(31) |
 .
.
Thevenin's theorem and Norton's theorem
In principle, all currents and voltages of an arbitrary network of linear components and voltage/current sources can be found by either the loop current method or the node voltage method, as we have seen previously.
However, if only the current 








Any one-port (two-terminal) network of resistance elements and energy
sources is equivalent to (can be modeled by) an ideal voltage source


 is the open-circuit voltage of the network,
is the open-circuit voltage of the network,
 is the equivalent resistance when all energy sources are
turned off (short-circuit for voltage sources, open-circuit for current
sources).
is the equivalent resistance when all energy sources are
turned off (short-circuit for voltage sources, open-circuit for current
sources).
Proof:

 at
the output port of the network are
at
the output port of the network are  and
and  , respectively.
, respectively.
 in circuit (a) by an ideal current source
in circuit (a) by an ideal current source
 while keeping voltage
while keeping voltage  the same (b), all voltages and
currents in the network to be modeled are not affected.
the same (b), all voltages and
currents in the network to be modeled are not affected.
 in terms of the internal energy sources inside
the network and the external current source by superposition principle:
in terms of the internal energy sources inside
the network and the external current source by superposition principle:
 due only to the energy
sources internal to the network (c).
due only to the energy
sources internal to the network (c).
 ,
where
,
where  is the equivalent resistance of the network with all energy
sources off, due only to the external current source (d).
is the equivalent resistance of the network with all energy
sources off, due only to the external current source (d).
 .
.
 and current
and current  in the circuit in (e) are also
related by the same equation
in the circuit in (e) are also
related by the same equation
 , i.e., this circuit
is equivalent to the original circuit in (a), and can therefore be
used as a model of the circuit.
, i.e., this circuit
is equivalent to the original circuit in (a), and can therefore be
used as a model of the circuit.
We see that as far as the port voltage 



Any one-port (two-terminal) network of resistance elements and energy
sources is equivalent to (can be modeled by) an ideal current source


 is the short-circuit current of the network
is the short-circuit current of the network
 is the same resistance as in Thevenin's theorem.
is the same resistance as in Thevenin's theorem.
Proof: The proof of this theorem is in parallel with the proof of Thevenin's theorem.

 at
the output port of the network are
at
the output port of the network are  and
and  , respectively.
, respectively.
 in circuit (a) by an ideal voltage source
in circuit (a) by an ideal voltage source
 while keeping current
while keeping current  the same (b), all voltages and currents
in the network to be modeled are not affected.
the same (b), all voltages and currents
in the network to be modeled are not affected.
 in terms of the internal energy sources inside
the network and the external voltage source by superposition principle:
in terms of the internal energy sources inside
the network and the external voltage source by superposition principle:
 due only to the energy
sources internal to the network (c).
due only to the energy
sources internal to the network (c).
 ,
where
,
where  is the equivalent resistance of the network with all energy
sources off, due only to the external voltage source (d).
is the equivalent resistance of the network with all energy
sources off, due only to the external voltage source (d).
 .
.
 and voltage
and voltage  in the circuit in (e) are also
related by the same equation
in the circuit in (e) are also
related by the same equation
 , i.e., this circuit
is equivalent to the original circuit in (a), and can therefore be
used as a model of the circuit.
, i.e., this circuit
is equivalent to the original circuit in (a), and can therefore be
used as a model of the circuit.
We see that as far as the port voltage 



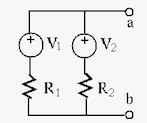
Moreover, we note that Thevenin's theorem and Norton's theorem are
equivalent, as one can always be converted into the other. The internal
resistances in both theorems are the same 




 |
(32) |
The voltage across a set of 



 |
(33) |
Proof: (Homework)
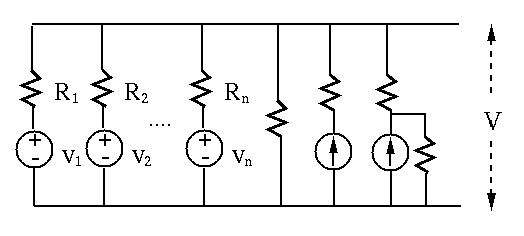
This theorem can be augmented to include branches containing 








 -Y Transformation
-Y Transformation
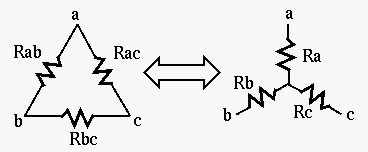
The 






 |
(34) |
 to
to  :
:
Given 








 |
(35) |
 to
to  :
:
Reversely, given 







 |
(36) |
The top circuit (a bridged T-network) in the following figure can be converted into either of the two equivalent circuits below.
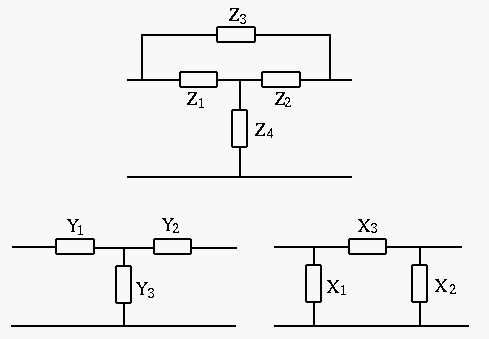
 formed by
formed by  ,
,  , and
, and  can be converted
to a Y, which can then be combined with
can be converted
to a Y, which can then be combined with  to get a Y (bottom left):
to get a Y (bottom left):
 |
(37) |
 ,
,  , and
, and  can be converted to a
can be converted to a
 , which can then be combined with
, which can then be combined with  to get a
to get a  (bottom right):
(bottom right):
 |
(38) |
 and Y circuits are equivalent as it can be
shown that they can also be converted to each other with the same
system variables.
and Y circuits are equivalent as it can be
shown that they can also be converted to each other with the same
system variables.
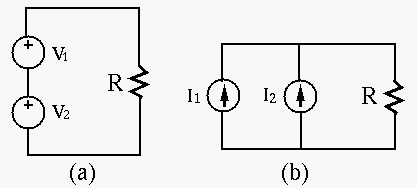
Example 1: Model the circuit in part (a) by Thevenin's theorem (b) and Norton's theorem (c).
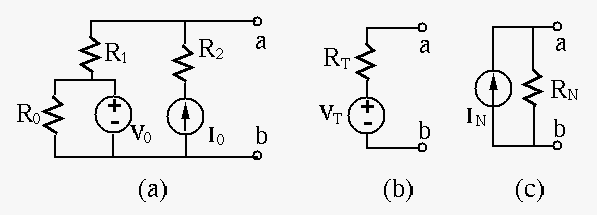
Find equivalent internal resistance when both energy sources
are turned off:

Find open-circuit voltage:

Find short-circuit current (superposition):

 |
(39) |
 and
and  do not appear in either of
the two equivalent circuits, because a voltage source provides a constant
voltage
do not appear in either of
the two equivalent circuits, because a voltage source provides a constant
voltage  independent of any resistance in parallel, and a current
source drives a constant current
independent of any resistance in parallel, and a current
source drives a constant current  , independent of any resistance
in series.
, independent of any resistance
in series.
Example 2: Find voltage 


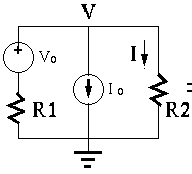
Any one of the following methods can be used to solve the circuit:
Apply KVL around the outer loop with loop current 
 |
(40) |
 |
(41) |
Assume the currents 



 i.e., i.e., |
(42) |
 , we get:
, we get:
 |
(43) |
 |
(44) |
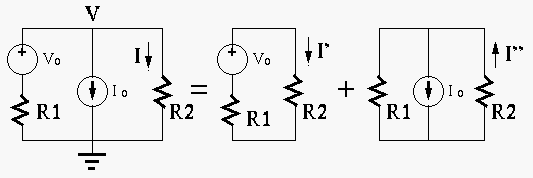
 and
and  with the current source off (open-circuit with
zero current):
with the current source off (open-circuit with
zero current):
 |
(45) |
 and
and  with the voltage source off (short-circuit with
zero voltage):
with the voltage source off (short-circuit with
zero voltage):
 |
(46) |
 and
and  have a negative sign as their direction and polarity
are opposite to those of the assumed current and voltage.
have a negative sign as their direction and polarity
are opposite to those of the assumed current and voltage.
 |
(47) |
 |
(48) |
 and
and  in the left branch as a non-ideal
voltage source into a current source
in the left branch as a non-ideal
voltage source into a current source
 (upward);
(upward);
 and
and  ;
;
 (current devider):
(current devider):
 |
(49) |
 :
:
 |
(50) |
 ,
,
 |
(51) |
 .
.
 |
(52) |
 |
(53) |
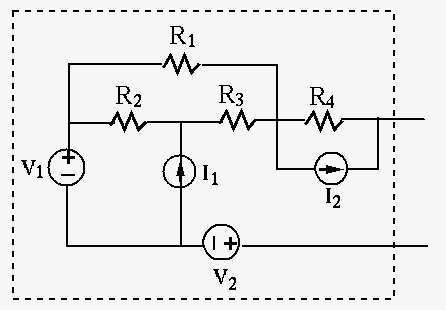
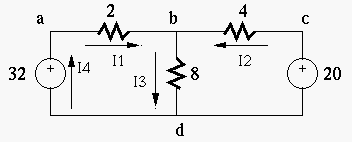
Example 3: In the circuit below, 










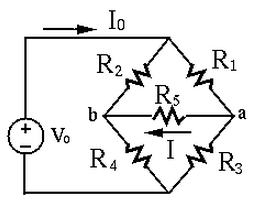
Consider three independent loops with clockwise loop currents:
 in the left loop (
in the left loop ( ,
,  ,
,  )
)
 in the top loop (
in the top loop ( ,
, ,
,  )
)
 in the bottom loop (
in the bottom loop ( ,
,  ,
,  )
)
 |
(54) |
 |
(55) |
 |
(56) |
 is
is
 or or |
(57) |
 to find
the current through it.
to find
the current through it.
Assume the bottom node is ground with 0 volt, then the voltage at
the top node is known to be 
 |
(58) |
 |
(59) |
 |
(60) |
 is
is
 |
(61) |
 to find
the current through it.
to find
the current through it.
To find 




 |
(62) |
 ,
,
 ,
and
,
and
 |
(63) |
 conversion
conversion
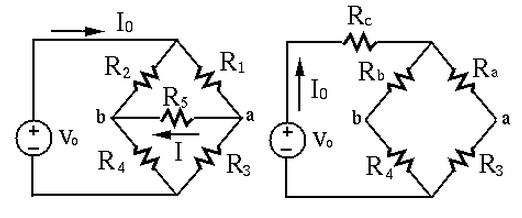
To find 









 |
(64) |
 :
:
 |
(65) |
 |
(66) |
 and
and  (current divider):
(current divider):
 |
(67) |
 |
(68) |
 and
and  (assuming the bottom node
is ground):
(assuming the bottom node
is ground):
 |
(69) |
 through
through
 :
:
 |
(70) |
For any of the methods above, the problem needs to be resolved
for




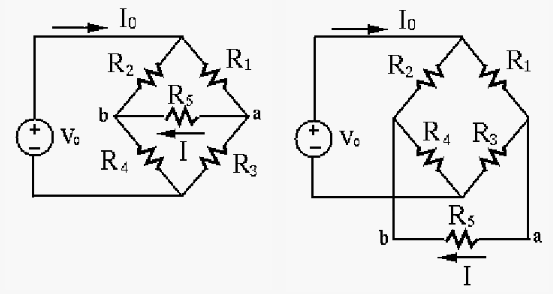
Solve the problem using Thevenin's theorem by the following steps:
 in series with an internal resistance
in series with an internal resistance  .
.
Specifically, we remove 





 |
(71) |
 short-circuit):
short-circuit):
 |
(72) |
 of different values can be found by
of different values can be found by
 |
(73) |
 ,
,

 ,
,

 ,
,

 ,
,

Example 4: The circuit below, often used in some control system, is composed of two voltages, two potentiometers, and a load resistor. Assume:
 |
(74) |
 through the load resistor
through the load resistor
 .
.
We denote the current through 




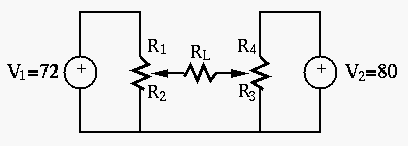
Superposition theorem
Find 




 . Assume
. Assume  , so that currents through
, so that currents through
 and
and  are
are  and
and  , respectively
(current divider), and
, respectively
(current divider), and
 .
.
 , current through
, current through  is
is
 , current through
, current through  is
is
 .
.
 . But
. But  ,
we get scaling factor
,
we get scaling factor
 , and
, and
 .
.
 . Assume
. Assume  , so that currents through
, so that currents through
 and
and  are, respectively,
are, respectively,  and
and  (current divider), and
(current divider), and
 .
.
 , current through
, current through  is
is
 , current through
, current through  is
is
 .
.
 . But
. But  ,
we get scaling factor
,
we get scaling factor
 , and
, and
 .
.
 |
(75) |
Thevenin's theorem
Remove 







 |
(76) |
Example 5: In the circuit below,









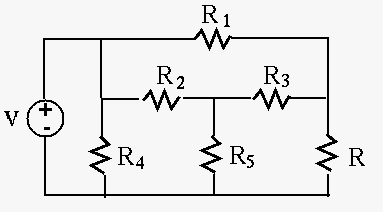
Node voltage method:
Let the voltages at the middle node be 

 |
(77) |
 ,
,  , and
, and
 .
.
Thevenin's theorem: (Homework)
Example 6: (Homework)
In the circuit below,