Next: Circuit Theorems Up: Chapter 2: Circuit Principles Previous: Chapter 2: Circuit Principles
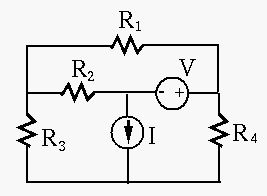
Example 1: Find the three unknown currents (


Note: The direction of a current and the polarity of a voltage can be assumed arbitrarily. To determine the actual direction and polarity, the sign of the values also should be considered. For example, a current labeled in left-to-right direction with a negative value is actually flowing right-to-left.
All voltages and currents in the circuit can be found by either of the following two methods, based on KVL or KCL respectively.
 independent loops in the circuit, define a
loop current around the loop in clockwise (or counter clockwise)
direction. These
independent loops in the circuit, define a
loop current around the loop in clockwise (or counter clockwise)
direction. These  loop currents are the unknown variables to
be obtained.
loop currents are the unknown variables to
be obtained.
 equations. While calculating the voltage
drop across each resistor shared by two loops, both loop currents
(in opposite positions) should be considered.
equations. While calculating the voltage
drop across each resistor shared by two loops, both loop currents
(in opposite positions) should be considered.
 equations for the
equations for the  unknown
loop currents.
unknown
loop currents.
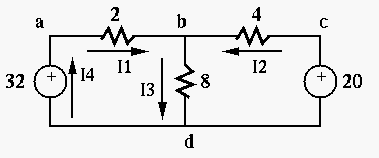
Find currents 


 and
and  around loops abda and bcdb
and apply the KVL to them:
around loops abda and bcdb
and apply the KVL to them:
 |
 |
 |
|
 |
 |
 |
(1) |
 |
(2) |
 ,
,
 , and
, and
 . Having
found
. Having
found  and
and  , we can easily find all voltages in the circuit:
, we can easily find all voltages in the circuit:
 ,
,
 ,
,  ,
,
 ,
,
 , and
, and
 .
.
 to get
three equations:
to get
three equations:
 |
 |
 |
|
 |
 |
 |
|
 |
 |
 |
(3) |
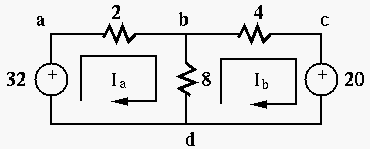
 and
and  around loops abda and bcdb:
around loops abda and bcdb:
 |
 |
 |
|
 |
 |
 |
(4) |
 |
(5) |
 and
and
 , same as the previous
results.
, same as the previous
results.
 nodes in the circuit. Select one of them
as the ground, the reference point for all voltages of the circuit.
The node voltage at each of the remaining
nodes in the circuit. Select one of them
as the ground, the reference point for all voltages of the circuit.
The node voltage at each of the remaining  nodes is an unknown
to be obtained.
nodes is an unknown
to be obtained.
 nodes to set the sum of all
currents into the node to zero, and get
nodes to set the sum of all
currents into the node to zero, and get  equations.
equations.
 equations for the
equations for the  unknown node voltages.
unknown node voltages.
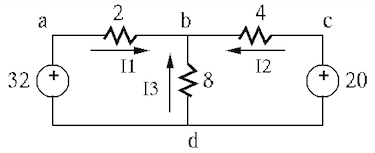
In the same circuit considered previously, there are only 2 nodes 







 |
(6) |
 |
(7) |
 ,
,  , and
, and  into the equation, we get
into the equation, we get
 |
(8) |
 , and all other currents and voltages can
be found subsequently:
, and all other currents and voltages can
be found subsequently:
 ,
,
 ,
,
 .
.
We could also apply KCL to node d, but the resulting equation is exactly
the same as

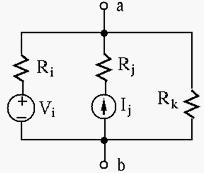
As special case of the node-voltage method with only two nodes, we have the following theorem:
If there are multiple parallel branches between two nodes 




Assume there are three types of branches:
 sources in series with
sources in series with  . The
polarity of each
. The
polarity of each  is + on the node a side.
is + on the node a side.
 (independent of resistors in series).
The direction of each
(independent of resistors in series).
The direction of each  is toward node a.
is toward node a.
 .
.
Applying KCL to node 
 |
(9) |
 , we get
, we get
 |
(10) |
 is the conductance.
is the conductance.
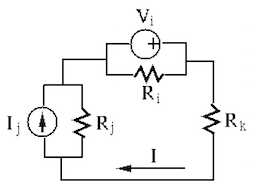
The dual form of the Millman's theorem can be derived based on the loop circuit on the right. Applying KVL to the loop, we have:
 |
(11) |
 , we get
, we get
 |
(12) |
Example 2: Solve the following circuit:
 ,
,  and
and  for loops 1 (top-left bacb), 2 (top-right adca), and 3 (bottom bcdb),
respectively, and applying KVL to the three loops, we get
for loops 1 (top-left bacb), 2 (top-right adca), and 3 (bottom bcdb),
respectively, and applying KVL to the three loops, we get
 |
(13) |
 |
(14) |
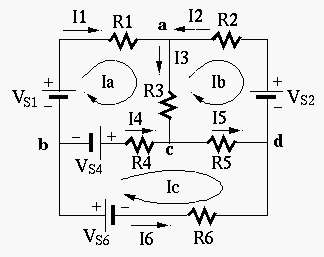
Example 3: Solve the following circuit with 





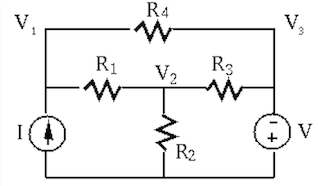
Assume three loop currents 





 |
(15) |
 |
(16) |



Assume the three node voltages with respect to the bottom node treated
as ground to be 





 |
(17) |
 |
(18) |
In other words, to simplify the analysis, it is preferable to
Example 4: In the circuit below, 





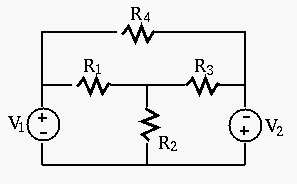
Find all node voltages with respect to the top-left corner treated
as the ground. Then do the same when the middle node where all three
resistors 


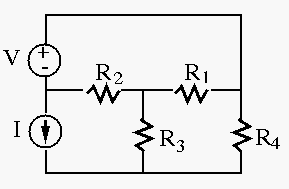
Example 5: The two circuits shown below are equivalent, but you
may want to choose wisely in terms of which is easier to analyze. Solve
this circuit using both node voltage and loop current methods. Assume