Next: Examples: Mechanical and Electrical Up: Chapter 1: Basic Quantities Previous: Resistor, Capacitor, and Inductor
The electric power associated with an element (R, C, or L) is the
product of the voltage 

 |
(37) |
 over a time period
over a time period  , we get the energy
, we get the energy
 |
(38) |
 , or stored in the element if
, or stored in the element if  . We
consider specifically the energy dissipation/storage in each of
the three types of elements
. We
consider specifically the energy dissipation/storage in each of
the three types of elements  ,
,  , and
, and  .
.

When a voltage 


 |
(39) |
 is
is
 |
(40) |
 .
.
 is applied across
is applied across  , the current
through it is
, the current
through it is  , and the power consumed by the resistor is
, and the power consumed by the resistor is
 |
(41) |
 is
is
 |
(42) |
 is applied
across
is applied
across  , the current through it is
, the current through it is
 ,
and the energy dissipated in time period
,
and the energy dissipated in time period
 is:
is:
![$\displaystyle w=\frac{1}{R}\int_0^T v^2(t) dt
=\frac{V_p^2}{R}\int_0^T \sin^2(\omega t) dt
=\frac{V_p^2}{2R}\int_0^T [1-\cos(2\omega t)] dt=\frac{V_p^2}{2R}\,T$](img178.svg) |
(43) |
 as the equivalent DC voltage needed for
as the equivalent DC voltage needed for  to dissipate the same amount
of energy as
to dissipate the same amount
of energy as
 :
:
 |
(44) |
 we get
we get
 |
(45) |
 when
either a sinusoidal voltage with peak amplitude
when
either a sinusoidal voltage with peak amplitude  or a DC voltage
or a DC voltage
 is applied across it.
is applied across it.
Some useful trigonometric identities:
![$\displaystyle \sin\alpha \cos\alpha=\frac{1}{2} \sin{2\alpha},\;\;\;
\sin^2\alpha =\frac{1}{2}[1-\cos(2\alpha)],\;\;\;
\cos^2\alpha =\frac{1}{2}[1+\cos(2\alpha)]$](img184.svg) |
(46) |
The average of a time varying current 



 i.e. i.e. |
(47) |
 |
(48) |
 |
(49) |
 is always zero (the
charge transferred during the first half is the opposite to that
transferred in the second). However, if we consider the half-cycle
over
is always zero (the
charge transferred during the first half is the opposite to that
transferred in the second). However, if we consider the half-cycle
over  , the average is:
, the average is:
 |
 |
 |
|
 |
![$\displaystyle \frac{I_p}{\pi}\left[\cos(0)-\cos(\pi)\right]
=\frac{2}{\pi}\,I_p=0.637\,I_p$](img195.svg) |
(50) |

Given voltage 


 |
(51) |
 and
and  .
.
If



 |
(52) |
 . In the first and third quarters of the period
. In the first and third quarters of the period  , the energy
is stored in the electric field of the capacitor (equivalent to a battery
being charged), but in the 2nd and 4th quarters of the period
, the energy
is stored in the electric field of the capacitor (equivalent to a battery
being charged), but in the 2nd and 4th quarters of the period  , the energy
is released from the capacitor to the rest of the circuit (equivalent to a
battery delivering power).
, the energy
is released from the capacitor to the rest of the circuit (equivalent to a
battery delivering power).

Given voltage 


 |
(53) |
 and
and  .
.
If



 |
(54) |
 of a sinusoidal voltage. In the first and third quarter of the period
of a sinusoidal voltage. In the first and third quarter of the period
 , the energy is stored in the magnetic field of the inductor, but in
the 2nd and 4th quarter of the period
, the energy is stored in the magnetic field of the inductor, but in
the 2nd and 4th quarter of the period  , the energy is released from the
inductor to the rest of the circuit.
, the energy is released from the
inductor to the rest of the circuit.
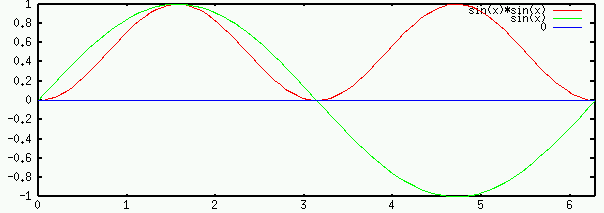
 or
or  out of phase. Specifically,
out of phase. Specifically,
 (red) lags the current
(red) lags the current
 (green) by
(green) by  (or
(or  ).
).
 (green) leads
the current
(green) leads
the current
 (red) by
(red) by  (or
(or  ).
).
The figure below illustrates the energy flow in a circuit involving capacitor and inductor, as energy storing components:
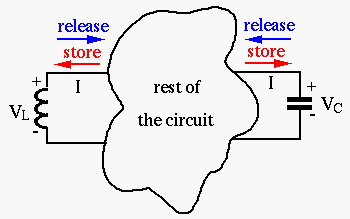
Comparison of Energy storage in mechanical and electromagnetic systems:
 and voltage
and voltage  :
:
 |
(55) |
![$\displaystyle [Farad][volt]^2=\frac{[Ampere][second]}{[Volt]}[Volt]^2$](img215.svg) |
|||
 |
![$\displaystyle [Ampere][Volt][second]=[Watt][second]=[Joule]$](img216.svg) |
(56) |
 and current
and current  :
:
 |
(57) |
![$\displaystyle [Henry][Ampere]^2=\frac{[Volt][second]}{[Ampere]}[Ampere]^2$](img218.svg) |
|||
 |
![$\displaystyle [Volt][Ampere][second]=[Watt][second]=[Joule]$](img219.svg) |
(58) |
 of 1 meter per second possesses 1/2 Joule
of kinetic energy.
of 1 meter per second possesses 1/2 Joule
of kinetic energy.
![$\displaystyle w=\frac{1}{2}mu^2,\;\;\;\;\;\frac{[kilogram][meter]^2}{[second]^2}=[Joule]$](img221.svg) |
(59) |
 cal
cal Joules
Joules
 )
of stiffness
)
of stiffness  or compliance
or compliance  is
is
![$\displaystyle w=\frac{1}{2}Cf^2=\frac{1}{2}K x^2,\;\;\;\;\;
\frac{[meter]}{[Newton]}[Newton]^2=[meter][Newton]=[Joule]$](img226.svg) |
(60) |