Resistor, Capacitor, and Inductor

In the following, we adopt the convention that a constant or direct current (DC) or voltage is represented by an upper-case letter $I$ or $V$, while a time-varying or alternating current (AC) current or voltage is represented by a lower-case letter $i(t)$ or $v(t)$, sometimes simply $i$ and $v$.

Each of the three basic components resistor R, capacitor C, and inductor L can be described in terms of the relationship between the voltage across and the current through the component:

• Resistor

  The voltage across and the current through a resistor are related by Ohm's law:

  $$R=\frac{V}{I}=\frac{v}{i},\;\;\;\;\;\;\;[Ohm]=\frac{[Volt]}{[Ampere]}, \;\;\;\;\;\;\; \Omega=\frac{V}{A}$$ (19)

  Here $R$ is the resistance of the conductor measured by Ohm $\Omega$ (George Ohm (1789-1854)).

  The reciprocal of the resistance is the conductance:

  $$G=\frac{1}{R}=\frac{I}{V}=\frac{i}{v},\;\;\;\;\;\;\; [Siemens]=\frac{1}{[Ohm]}=\frac{[Ampere]}{[Volt]}, \;\;\;\;\;\;S=\frac{1}{\Omega}=\frac{A}{V}$$ (20)

  Conductance is measured by $[Siemens]=1/[Ohm]$ or $S=1/\Omega$ (Werner von Siemens (1816-1892))

• Capacitor

  A capacitor is composed of a pair of conductor plates separated by some insulation material. The same amount of charge $Q$ (of opposite polarity) is stored on each of the two plates.

  

  

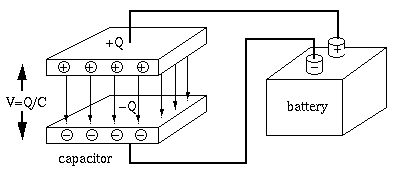
  The voltage $V$ between the two plates is proportional to the charge $Q$, but inversely proportional to the capacitance $C$ of the capacitor:

  $$V=\frac{Q}{C},\;\;\;\;\;\;\;Q=VC,\;\;\;\;\;\;\; C=\frac{Q}{V}$$ (21)

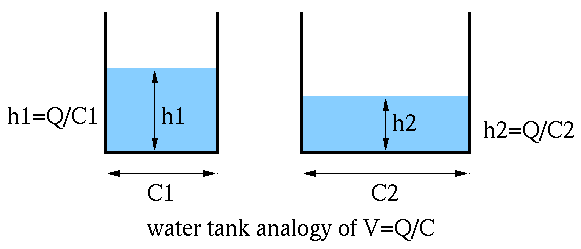
  This relationship can be understood by considering the water tank analogy of the capacitor. The capacity $C_1$ (analogous to capacitance of a capacitor) of the tank on the left is smaller than that of $C_2$ on the right, for the same amount of water $Q$ (analogous to charge), the water surface $h_1$ is higher than that of $h_2$, indicating the surface height $h_1$ (analogous to voltage $V$) is proportional to water volume $Q$ but inversely proportional to the tank capacity $C$, i.e., $V=Q/C$.

  

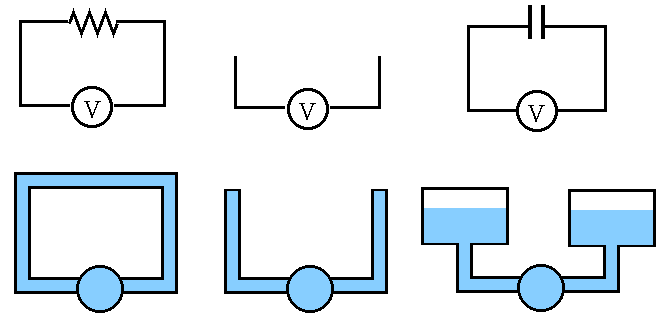
  Why can an AC current “flow through” a capacitor composed of two insulated plates? Again consider the water tank analogy of the capacitor. If the pipeline is disconnected (an open circuit), no water flow (current) can go through. If two tanks are connected to the ends of the pipeline (a capacitor), and the pump drives the water in one direction (analogous to a DC voltage source), one of the tanks will fill up while the other one is empty (due to some initial current), there is still no continuous current. However, if the pump drives the water in alternative directions (analogous to AC voltage source), the water can flow through the pipeline, analogous to an AC current going through a capacitor (not through the insulation between its two plates).

  The current through a capacitor can be found as:

  $$i(t)=\frac{dq(t)}{dt}=\frac{dq}{dv}\,\frac{dv}{dt}=C\frac{dv(t)}{dt}, \;\;\;\;\;\;\; v(t)=\frac{q(t)}{C}=\frac{1}{C}\int_{-\infty}^t i(\tau) d\tau,$$ (22)

  where $q=\int_{-\infty}^t i(\tau)\,d\tau$, and the capacitance $C=dq/dv$ represents the capacitor's capability to store charge per unit voltage. Capacitance $C$ is determined by the parameters of the capacitor:

  $$C=\frac{\epsilon A}{d}=\frac{\epsilon_0\epsilon_r A}{d}$$ (23)

  where $A$ is the overlapping area of the plates and $d$ is the distance between them, while $\epsilon$ is the permittivity (dielectric constant) (the amount of charge needed to generate one unit of electric flux) of the medium between the plates, $\epsilon_0=8.854\times 10^{-12} F/m$ is the vacuum permittivity, and $\epsilon_r=\epsilon/\epsilon_0$ is the relative permitivity. In an electrolytic capacitor, the gap between the two plates is filled with dielectric medium of higher permittivity so that the capacitance $C$ is increased.

  $C$ is measured in Farads (F) (Michael Faraday (1791-1867)):

  $$[Farad]=\frac{[Ampere][second]}{[Volt]} =\frac{[Coulomb]}{[Volt]}, \;\;\;\;\;\;\; F=\frac{A\;s}{V}=\frac{C}{V}$$ (24)

  Other units also used for capacitance include $\mu F=10^{-6} F$, $nF=10^{-9}F$, and $pF=10^{-12}F$.

  Specially, when the voltage is sinusoidal $v(t)=sin(\omega t)$, the current is

  $$i(t)=C \frac{d\,v(t)}{dt}=C \frac{d\sin(\omega t)}{dt} =\omega C\;\cos(\omega t)$$ (25)

  

  1. The current (red) has a 90 degree phase lead compared to the voltage (green), as it takes time for the voltage across the capacitor to build up;
  2. The amplitude of the current is proportional to the frequency $\omega=2\pi f$ of the voltage. In particular, for DC ($\omega=0$). The current $i(t)=\omega C\cos(\omega t)$ is 0 (open circuit), and when the frequency is very high ( $\omega \rightarrow \infty$), the current $i(t)=\omega C\cos(\omega t) \rightarrow \infty$ (short circuit).

• Inductor
  • Electromagnetic Interaction: Electricity to Magnetism

    Magnetic field (flux) is generated in the space around a current flowing through a piece of conductor:

    

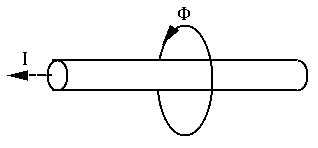
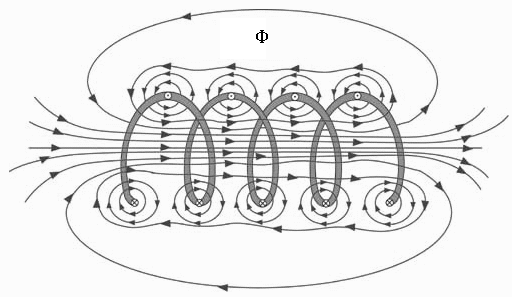
    The magnetic field around a coil is the superposition of the magnetic flux generated by each section of the coil:

    

  • Electromagnetic Interaction: Magnetism to Electricity

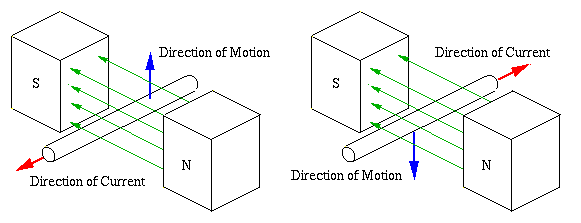
    Electric current is induced in a conductor when there is changing magnetic flux in the surrounding space.

    

    

  • Self and Mutual Induction

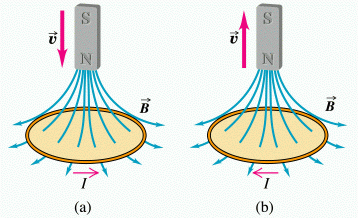
    A time-varying electric current in a coil will cause a time-varying magnetic field in the surrounding space, which in turn will induce electric voltage and then current in the same coil (self-induction) or a different coil in the neighborhood (mutual-induction).

  • Faraday's Law:

    The self-induced voltage, the electromotive force (emf), across the inductor coil due to a current $i(t)$ is proportional to the rate of change of the total magnetic flux $\Psi=N\Phi$ ($\Phi$ being the flux in one of the $N$ turns of the coil) caused by the current $i(t)$:

    $$v(t)=\frac{d\Psi(t)}{dt}=\frac{d\Psi}{di}\frac{di}{dt}=L\frac{di}... ... \;\;\;\;\;\;\;\; i(t)=\frac{1}{L}\int_{-\infty}^t v(\tau) d\tau=\frac{\Psi}{L}$$ (26)

    where $\Psi=\int_{-\infty}^t v(\tau)\,d\tau$, and $L=d\Psi/di$ is the inductance of the inductor representing its capability to produce magnetic flux per unit current. Inductance $L$ is determined by the parameters of the inductor:

    $$L=\frac{\mu N^2 A}{l}$$ (27)

    where $A$ and $l$ are respectively the cross section area and length of the coil, $N$ is the number of turns, and $\mu$ is the magnetic permeability (the ability of a material to support the formation of a magnetic field within itself) of the medium inside the coil. When a medium of high permeability, such as an iron core, is inserted into the coil, its inductance $L$ is increased.

    The unit of $L$ is henrys (H) (Joseph Henry (1797-1878)):

    $$[Henry]=\frac{[Volt][second]}{[Ampere]}, \;\;\;\;\;\;\; H=\frac{Vs}{A}$$ (28)

    Other units also used for $L$ include $mH=10^{-3}H$ and $\mu H=10^{-6}H$.

  • Lenz's Law:

    The polarity of the self-induced voltage $v(t)$ in a coil is such that it tends to produce a current which induces a magnetic flux to oppose the change of the magnetic field that induced the voltage, thereby opposing any change in current $i(t)$ that is causing the magnetic flux.

    When current $i(t)$ increases, the induced voltage $v(t)$ tends to resist it, when current $i(t)$ decreases, the induced voltage $v(t)$ tends to sustain it.

  Specially, when the current is sinusoidal $i(t)=sin(\omega t)$, the voltage is

  $$v(t)=L \frac{d\,i(t)}{dt} =L \frac{d\,\sin(\omega t)}{dt} = \omega L\;\cos(\omega t)$$ (29)

  

  1. The current (red) has a 90 degree phase lag compared to the voltage (green) as it takes time to overcome the counter potential of the inductor for the current to flow;
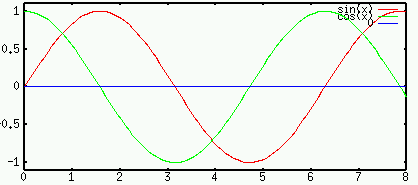
  2. The amplitude of the voltage is proportional to the frequency $\omega=2\pi f$ of the current. In particular, for DC ($\omega=0$), the voltage is 0 (short circuit), and when the frequency is very high ( $\omega \rightarrow \infty$), the voltage $i(t) \rightarrow 0$ (open circuit) for a finite $v(t)$.

  From the above discussion, we see that for sinusoidal voltage and current, the voltage across a capacitor is lagging behind the current by 90 degrees, as it takes time to build up the charge $Q=\int i\;dt$ and thereby the voltage $V_C=Q/C$; while the current through an inductor is lagging behind the voltage across it, as it takes time to build up the magnective flux $\Psi=\int v\;dt$ and thereby the current $i=\Psi/L$. This fact can be easily memorized by “ELI the ICE man” (E for electromotive force (emf) is the same as voltage and I for current).

  Note the following dimensionalities:

  $$\left[\sqrt{\frac{L}{C}}\right]=\sqrt{\frac{[Henry]}{[Farad]}} =\... ...nd]}{[Ampere]}\frac{[Volt]}{[second]\;[Ampere]}} =\frac{[Volt]}{[Ampere]}=[Ohm]$$ (30)

  $$\left[ \sqrt{LC} \right]=\sqrt{[Henry]\;[Farad]} =\sqrt{\frac{[Volt]\;[second]}{[Ampere]}\frac{[Ampere]\;[second]}{[Volt]}} =[second]$$ (31)

  Comparing the relationships between the current through and voltage across the three components below, we see that capacitance $C$ is a conductive variable similar to $G$, while inductance $L$ is a resistive variable similar to $R$.

  Resistor	$i=v/R=Gv$	$v=Ri=i/G$
  Inductor	$i=\int v\,dt/L$	$v=L\;di/dt$
  Capacitor	$i=C\,dv/dt$	$v=\int i\,dt/C$

• Ideal Transformer

  

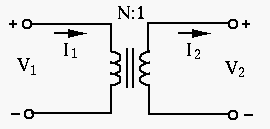
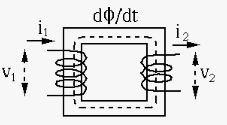
  Two coils around a common iron core form a transformer. Assume the primary coil has $N_1$ turns of wire and the secondary coil has $N_2$ turns. The total magnetic flux $\Psi=N\Phi$ is proportional to the number of turns $N$, where $\Phi$ is the flux with one turn of wire in both primary and secondary coils. We assume the transformer is ideal or lossless, in the sense that

  • There is no flux loss. The same flux $\Phi$ goes through the iron core of both primary and secondary coils;
  • There is no power loss, the power $p$ received by the primary coil is is completely delivered to the secondary coil.

  Faraday's Law: The voltage across a coil is proportional to the rate of change of the total magnetic flux:

  $$v_1(t)=\frac{d\Psi_1}{dt}=N_1\frac{d\Phi}{dt},\;\;\;\;\;\; v_2(t)=\frac{d\Psi_2}{dt}=N_2\frac{d\Phi}{dt}$$ (32)

  i.e.,

  $$\frac{v_2}{v_1}=\frac{N_2}{N_1}$$ (33)

  Also, as there is no power loss in an ideal transformer, the powers on both the primary and secondary sides are the same:

  $$p_1=v_1 i_1=p_2=v_2 i_2,\;\;\;\;\; \;\;\;\;\;\;\; \frac{i_1}{i_2}=\frac{v_2}{v_1}=\frac{N_2}{N_1}$$ (34)

  from which we get:

  $$v_2=\frac{N_2}{N_1} v_1,\;\;\;\;\;\;\;i_2=\frac{N_1}{N_2} i_1$$ (35)

  If we assume the secondary side is connected to a load resistance $R_L$, then according Ohm's law, we have $v_2/i_2=R_2$, and

  $$\frac{v_1}{i_1}=\frac{(N_1/N_2)v_2}{(N_2/N_1)i_2} =\left(\frac{N_1}{N_2}\right)^2 \frac{v_2}{i_2} =\left(\frac{N_1}{N_2}\right)^2 R_L=R'_L$$ (36)

  which is the equivalent resistance that appears on the primary side.