


Next: Phase Plane
Up: DEsystem
Previous: Nonhomogeneous DE System
Consider a nonlinear first order ODE system:
If we define
then the system can be written in matrx form as
which can be further expressed in Taylor series around a specific
point
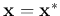 containing the constant (zero order) term,
first order term, and all the higher order terms:
containing the constant (zero order) term,
first order term, and all the higher order terms:
where
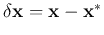 and
and 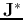 is the
Jacobian matrix of the vector function
is the
Jacobian matrix of the vector function
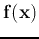 evaluated at
evaluated at
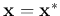 :
:
We also note that
and the equation above can be written as
We assume 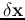 is small, then we can neglect all higher
order terms than first order in the Taylor expansion and get
is small, then we can neglect all higher
order terms than first order in the Taylor expansion and get
If we further let 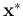 be the equilibrium point of
the system, i.e.,
be the equilibrium point of
the system, i.e.,
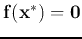 , then the equation
above becomes a first order homogeneous LCCODE system:
, then the equation
above becomes a first order homogeneous LCCODE system:
The solution of this system is in the form of
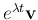 ,
where
,
where 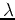 is an eigenvalue of
is an eigenvalue of 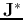 and
and 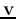 is
the corresponding eigenvector, satisfying
is
the corresponding eigenvector, satisfying
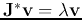 . In general, such an eigenvalue
is complex and can be written in terms of its real and imaginary
parts,
. In general, such an eigenvalue
is complex and can be written in terms of its real and imaginary
parts,
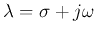 , and the general solution can be
written as
, and the general solution can be
written as
If
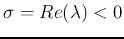 , the magnitude of the solution
, the magnitude of the solution 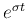 will attenuate to zero, i.e., the system is stable; however, if
will attenuate to zero, i.e., the system is stable; however, if
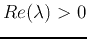 , the magnitude of the solution
, the magnitude of the solution 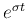 will
grow without a bound, i.e., the system is unstable.
will
grow without a bound, i.e., the system is unstable.
As we only keep a locally linear approximation around the
equilibrium point, the corresponding analysis of the system
is a linear stability analysis, which describes the
behavior of the system close to the equilibrium point.



Next: Phase Plane
Up: DEsystem
Previous: Nonhomogeneous DE System
Ruye Wang
2019-02-21
![\begin{displaymath}
{\bf x}=\left[\begin{array}{c}x_1 \vdots x_n\end{array}\...
...1,\cdots,x_n) \vdots f_n(x_1,\cdots,x_n)\end{array}\right]
\end{displaymath}](img154.png)
![\begin{displaymath}
{\bf J}^*={\bf J}({\bf x}^*)=\left[\begin{array}{ccc}\frac{\...
...tial f_n}{\partial x_n}
\end{array}\right]_{{\bf x}={\bf x}^*}
\end{displaymath}](img161.png)