


Next: About this document ...
Up: DEsystem
Previous: Stability Analysis of Nonlinear
Consider a first order LCCODE system containing 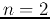 variables:
variables:
The general solution is
where 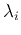 and
and 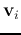 are the eigenvalue and corresponding
eigenvectors of
are the eigenvalue and corresponding
eigenvectors of 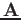 satisfying
satisfying
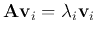 .
Specifically, these eigenvalues can be found by solving the following
characteristic polynomial:
.
Specifically, these eigenvalues can be found by solving the following
characteristic polynomial:
where
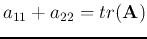 and
and
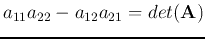 are the trace and determinant of
are the trace and determinant of  respectively.
Solving the equadratic equation, we get the two roots:
respectively.
Solving the equadratic equation, we get the two roots:
where
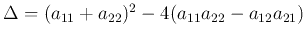 .
.
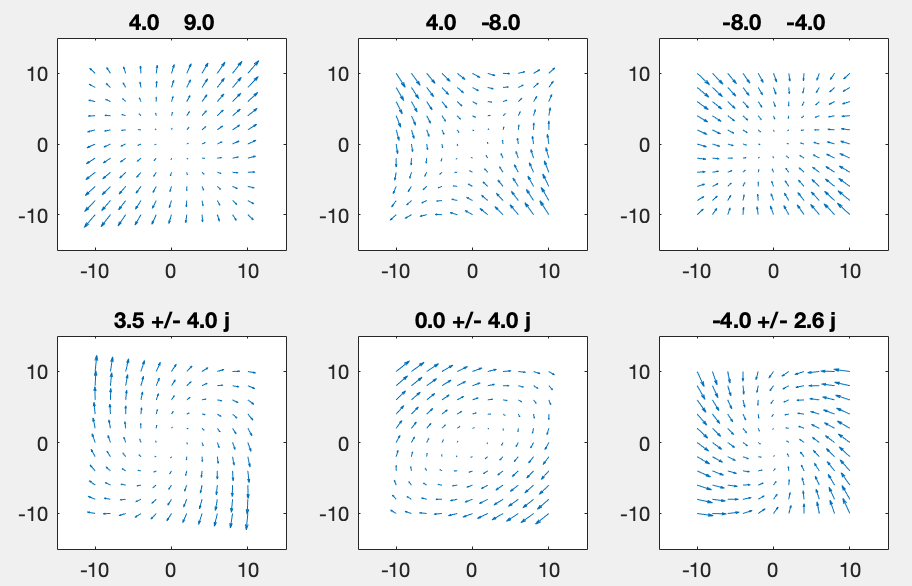
-
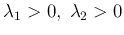 unstable
unstable
-
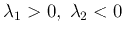 saddle point
saddle point
-
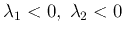 stable
stable
-
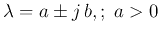 unstable, spiral out
unstable, spiral out
-
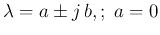 marginal stable
marginal stable
-
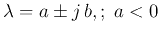 stable, spiral in
stable, spiral in
Ruye Wang
2019-02-21
![]() variables:
variables:
![\begin{displaymath}
\dot{\bf x}=\left[\begin{array}{c}\dot{x}_1 \dot{x}_2\end{...
...gin{array}{c}\dot{x}_1 \dot{x}_2\end{array}\right]
={\bf Ax}
\end{displaymath}](img177.png)
![\begin{displaymath}
\left[\begin{array}{rr}6&2\\ 3&7\end{array}\right],\;\;\;
\l...
...],\;\;\;
\left[\begin{array}{rr}-5&-2\\ 4&-3\end{array}\right]
\end{displaymath}](img187.png)

