


Next: Nonhomogeneous DE System
Up: DEsystem
Previous: Homogeneous DE System
Based on the Taylor expansion of the exponential function of a
scalor variable:
we can also define the exponential function of a matrix 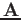 as
as
In particular, when
 , we get
, we get
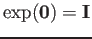 .
.
Consider the eigenequation of 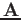 :
:
These 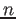 equations can be combined to become
equations can be combined to become
we therefore also have
i.e., in general,
Now r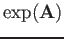 can be written as:
can be written as:
Ruye Wang
2019-02-21
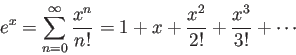
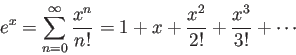
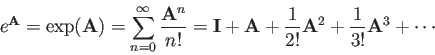
![]() :
:
![\begin{displaymath}
{\bf AV}={\bf A}[{\bf v}_1,\cdots,{\bf v}_n]=[{\bf v}_1,\cdo...
...s&\vdots 0&\cdots&\lambda_n\end{array}\right]={\bf V\Lambda}
\end{displaymath}](img97.png)
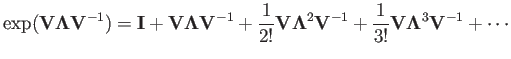
![$\displaystyle {\bf V}\left[{\bf I}+{\bf\Lambda}+\frac{1}{2!}{\bf\Lambda}^2+\fra...
...}{\bf\Lambda}^3
+\cdots\right]{\bf V}^{-1}
={\bf V}e^{\bf\Lambda}{\bf V}^{-1}$](img103.png)
![$\displaystyle {\bf V}\left[\begin{array}{ccc}e^{\lambda_1}&\cdots&0 \vdots&\ddots&\vdots 0&\cdots&e^{\lambda_n}\end{array}\right]{\bf V}^{-1}$](img104.png)