


Next: Homogeneous DE System
Up: DEsystem
Previous: Linear Constant Coefficient ODE
We consider solving an Nth-order single-variable explicit ODE
in the following form
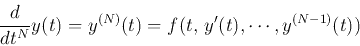 |
(1) |
We first convert the Nth order DE into a set of 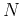 first order ODEs
by defining
first order ODEs
by defining
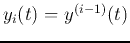 (
(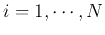 ). These
). These 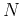 functions
can be represented in vector form:
functions
can be represented in vector form:
![\begin{displaymath}
{\bf y}(t)=\left[\begin{array}{c}y_1(t) y_2(t) y_3(t)\\...
...2(t) \vdots y'_{N-2}(t) y'_{N-1}(t)
\end{array} \right]
\end{displaymath}](img40.png) |
(2) |
Now the Nth-order ODE can be written as
and converted into a set of 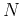 first-order differential equations:
first-order differential equations:
![\begin{displaymath}
\frac{d}{dt}{\bf y}(t)={\bf y}'(t)
=\left[\begin{array}{c}y'...
... f(t, {\bf y}(t))\end{array}\right]
={\bf f}(t, {\bf y}(t))
\end{displaymath}](img45.png) |
(4) |
This ODE system can then be solved as a special case of an ODE system of
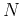 simultaneous first-order ODEs.
simultaneous first-order ODEs.
In the special case of an Nth order LCCODE:
where 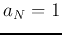 . We define
. We define
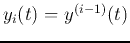 and get
and get
which can be written in matrix form as



Next: Homogeneous DE System
Up: DEsystem
Previous: Linear Constant Coefficient ODE
Ruye Wang
2019-02-21
![\begin{displaymath}
{\bf y}(t)=\left[\begin{array}{c}y_1(t) y_2(t) y_3(t)\\...
...2(t) \vdots y'_{N-2}(t) y'_{N-1}(t)
\end{array} \right]
\end{displaymath}](img40.png)
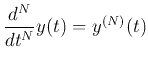
![\begin{displaymath}
\frac{d}{dt}{\bf y}(t)={\bf y}'(t)
=\left[\begin{array}{c}y'...
... f(t, {\bf y}(t))\end{array}\right]
={\bf f}(t, {\bf y}(t))
\end{displaymath}](img45.png)
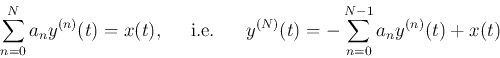
![\begin{displaymath}
\frac{d}{dt}{\bf y}(t)=\dot{\bf y}(t)
=\left[\begin{array}...
...}{c}0 0 0 \vdots 0 x(t)\end{array}\right]
\nonumber
\end{displaymath}](img48.png)