


Next: Differential Equation System
Up: DEsystem
Previous: DEsystem
We first consider the complete solution of a first order LCCODE:
is
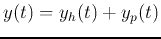 , the sum of the homogeneous solution
, the sum of the homogeneous solution
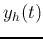 and a particular solution
and a particular solution 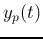 .
.
- To find
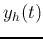 that satisfies the homogeneous DE
that satisfies the homogeneous DE
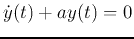 , we assume
, we assume
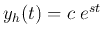 , and substitute
it together with
, and substitute
it together with
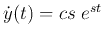 into the DE and get
into the DE and get
Dividing both sides by
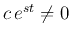 , we get
, we get 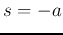 , i.e,
, i.e,
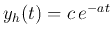 . To determine the coefficient
. To determine the coefficient 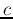 , we evaluate
, we evaluate
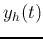 at
at  and get
and get
where 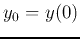 is the initial condition assumed to be given.
Then we have
is the initial condition assumed to be given.
Then we have
- To find the complete solution, we multiply both sides of the
ODE by
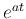 and get
and get
which can be rewritten as
Integrating both sides we get
Multiplying both sides by 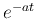 and rearranging, we get the
expression for
and rearranging, we get the
expression for 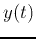
where
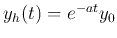 is the homogeneous solution found
above, and
is the homogeneous solution found
above, and
In particular, if the input
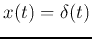 is an impulse,
we get the output
is an impulse,
we get the output 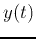 as the impulse response to be
as the impulse response to be
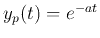 . We therefore see that in general, the particular
solution is the convolution of the impulse response
. We therefore see that in general, the particular
solution is the convolution of the impulse response 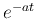 and
the input
and
the input 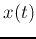 .
.
The DE can also be solved in s-domain based on Laplace transform.
Taking Laplace transform on both sides of the DE, we get
Solving for 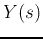 we get
we get
Taking inverse transform we get
We next consider the complete solution of a second order LCCODE
in the following canonical form:
Same as in the first order case, the complete solution of this
second order LCCODE is composed of the
homogeneous solution 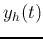 when
when 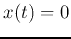 , and the
particular solution
, and the
particular solution 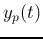 when
when 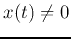 .
.



Next: Differential Equation System
Up: DEsystem
Previous: DEsystem
Ruye Wang
2019-02-21
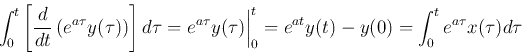
![\begin{displaymath}
y(t)={\cal L}^{-1} \left[\frac{y_0}{s+a}\right]
+{\cal L}^{-1}\left[ \frac{X(s)}{s+a}\right]
=y_0e^{-at}+x(t)\;*\;e^{-at}
\end{displaymath}](img32.png)