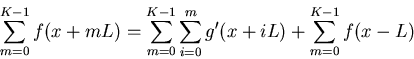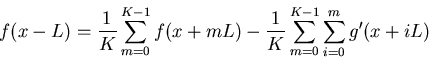Next: Numerical Derivatives
Up: No Title
Previous: Restoration by Inverse Filtering
To simplify the problem we assume:
- The image is blurred by linear motion:
where v is the constant speed of the motion and L=vT
is the distance traveled during the exposure time T.
- The width of the image W is a multiple of L:
W=KL
We next introduce a new variable x'=x-vt, and have
t=(x-x')/v and
dt=-dx'/v. Moreover, the integral limits 0 and T for t become,
respectively, x and x-vT=x-L for x'. Now the image becomes
where
For convenience, we will ignore the constant factor 1/v.
As the motion distortion is essentially an integration
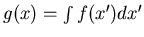 ,
to restore f(x) from g(x), we can simply differentiate g(x):
,
to restore f(x) from g(x), we can simply differentiate g(x):
and restore the original signal f(x) as
Note that above equation only recovers f(x) inside the interval
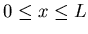 .
.
To recover the rest of f(x), we replace x by x+mL for
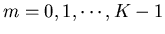 and apply the above relationship recursively
and apply the above relationship recursively
| f(x+mL) |
= |
g'(x+mL)+f(x+(m-1)L) |
|
| |
= |
g'(x+mL)+g'(x+(m-1)L)+f(x+(m-2)L) |
|
| |
= |
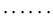 |
|
| |
= |
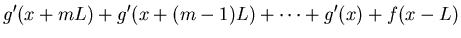 |
|
| |
= |
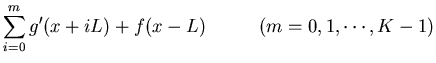 |
|
Here f(x-L) represents the segment of signal of length L that moves
from outside the image into the image during the exposure time T. If
f(x-L) is known, for example, if we can assume
f(x-L)=constant (e.g.,
uniform background), then the original signal f(x) over the entire interval
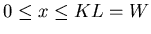 can be obtained by evaluating the above equation at
can be obtained by evaluating the above equation at
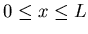 for all
for all
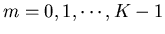 .
.
However, if we cannot assume
f(x-L)=constant, it need be estimated. As
the above equation is valid for
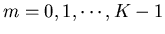 ,
we actually have K
equations which can be added up to give
,
we actually have K
equations which can be added up to give
which can be solved for f(x-L)
The first term on the right is an average of f(x) over the entire range of
the image and can be estimated by the average of g(x).



Next: Numerical Derivatives
Up: No Title
Previous: Restoration by Inverse Filtering
Ruye Wang
2000-03-31
![]() ,
to restore f(x) from g(x), we can simply differentiate g(x):
,
to restore f(x) from g(x), we can simply differentiate g(x):
![]() and apply the above relationship recursively
and apply the above relationship recursively
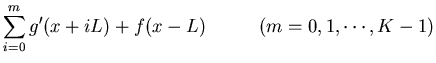
![]() ,
we actually have K
equations which can be added up to give
,
we actually have K
equations which can be added up to give