Numerical Derivatives

• Goal:

  Given a set of n+1 points $\{ (x_i, y_i),\;\;\;\vert\;\;\;(i=0,\cdots,n \}$, we want to estimate the derivative dy/dx at these points.

• Lagrange interpolation: We first reconstruct a continuous function y=f(x) so that
  
  $$f(x_i)=y_i\;\;\;\;\;\;\;\;\;\; (i=0,\cdots,n)$$
  
  
  using Lagrange formula:
  
  $$P_n(x)=\sum_{i=0}^n \prod_{(j=0, j \neq i)}^n\frac{ (x-x_j)}{(x_i-x_j)} y_i$$
  
  
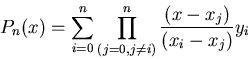
  P_n(x) is a polynomial function of x of order n which passes through all given points, i.e., $P_n(x_i)=y_i,\;\;\;(i=0,\cdots,n)$.

  For example, when n=2, we have
  

  $$P_3(x)=\frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}y_0+ \frac{(... ...0)(x_1-x_2)}y_1+ \frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}y_2$$
  
  

• Derivative estimation:

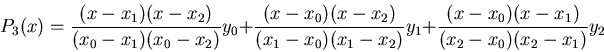
  Now the numerical derivative can be found by differentiating P_n(x). For example,
  

  $$P'_3(x)=\frac{2x-x_1-x_2}{(x_0-x_1)(x_0-x_2)}y_0+ \frac{2x-x... ...1-x_0)(x_1-x_2)}y_1+ \frac{2x-x_0-x_1}{(x_2-x_0)(x_2-x_1)}y_2$$
  
  

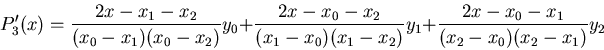
  Specially when the x_i's are equally spaced, i.e. x_i-1-x_i=h, the estimated derivative at x=x₀ can be found to be
  

  p'₃(x₀)=(-3y₀+4y₁-y₂)/2h
  
  
  It can be shown that the error is $h^2\;f^{'''}(\xi)/3$. Here f'(x₀) is estimated using 3 points (x₀, y₀), (x₁, y₁), (x₂, y₂) and is therefore called the forward estimation.

  We can also get backward estimation of f'(x₀) using (x₀, y₀), (x_-1, y_-1), (x_-2, y_-2):

  
  

  p'₃(x₀)=(3y₀-4y₁+y₂)/2h
  
  

  The average of the forward and backward estimations can be used as the final estimation of f'(x₀).

  To overcome possible noise, better estimation may be obtained by using more points, such as 4 or 5 points.

  The four-point forward estimation:
  

  p'₄(x₀)=(2y₃-9y₂+18y₁-11y₀)/6h
  
  
  The four-point forward estimation:
  
  p'₄(x₀)=(-2y_-3+9y_-2-18y_-1+11y₀)/6h
  
  

  The five-point forward estimation:
  

  p'₅(x₀)=(-3y₄+16y₃-36y₂+48y₁-25y₀)/12h
  
  
  The five-point backward estimation:
  
  p'₅(x₀)=(3y_-4-16y_-3+36y_-2-48y_-1+25y₀)/12h
  
  

  This method is based on the assumption that the function y=f(x) is continuous and noise-free. If this is not the case, the estimation error could be large.