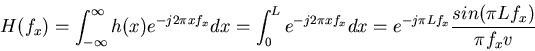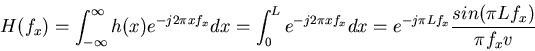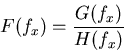Restoration by Inverse Filtering

Taking Fourier transform of the above convolution, we get

G(f_x)=F(f_x)H(f_x)

where G, F, and H are the spectra of g, f and h, respectively. Specifically, we have

$$H(f_x)=\int_{-\infty}^{\infty} h(x) e^{-j2\pi x f_x} dx =\int... ...\pi x f_x} dx = e^{-j\pi Lf_x}\frac{sin(\pi L f_x)}{\pi f_x v}$$

While the inverse filtering method could be applied to restore f(x) by inverse transforming F(f_x)

$$F(f_x)=\frac{G(f_x)}{H(f_x)}$$

we also realize that those points of F(f_x) corresponding to H(f_x)=0at 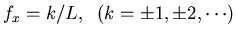$f_x=k/L,\;\;(k=\pm 1, \pm 2, \cdots)$ can never be restored. Interpolation from the neighboring points would not work (why?).

Moreover, this inverse filtering method is sensitive to noise that may exist in the imaging process.