Gabor model of V1 cells III - Temporal Domain

To model the temporal as well as spatial behavior of the cells, we first consider reducing the spatial dimension from 2 to 1 by replacing $y$, one of the two spatial variables of the 2D space, by the time variable $t$, and obtain this 2D spatiotemporal Gabor model:

$$G(x,t)=exp(-\frac{ x^2 }{2\sigma_x^2} -\frac{ t^2 }{2\sigma_t^2} ) \mbox{ } exp(j \omega_x x + j \omega_t t )$$

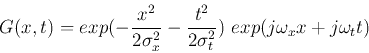
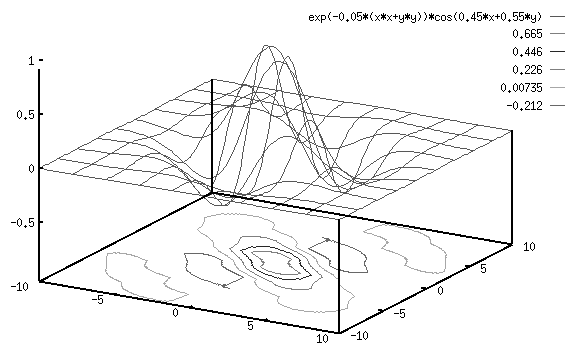
The plot of this 2D spatiaotemporal Gabor function $G(x,t)$ looks essentially the same as the plot of the 2D spatial Gabor function $G(x,y)$ shown before, with the only difference that the function's orientation in the 2D space now represents the cell's preferred motion speed (distance in $x$ over time $t$), instead of the preferred spatial orientation (slope or ratio of distance in $x$ over distance in $y$). These two 2D Gabor functions $G(x,y)$ and $G(x,t)$ therefore unify the treatment of spatial and spatiotemporal aspects of the response selectivity of the V1 cells.

If we keep both dimensions of the 2D spatial Gabor function and combine it with the temporal Gabor function, a 3D spatiotemporal Gabor filter is obtained which models both spatial orientation tuning and motion velocity (both direction and speed) tuning:

$$G(x,y,t)=exp(-\frac{ \vert {\bf r} \vert ^2 }{2\sigma_s^2} -... ...) \mbox{ } exp(j {\bf r} \cdot {\bf\omega_s} + j \omega_t t )$$

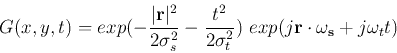
The Fourier spectrum of this spatiotemporal Gabor model can be found to be

$${\bf G}(\omega_x, \omega_y, \omega_t)= c\mbox{ }exp(-\frac... ... \mbox{ }exp(-\frac{\sigma_t^2 (\omega_t-\omega_{t0} )^2}{2} )$$

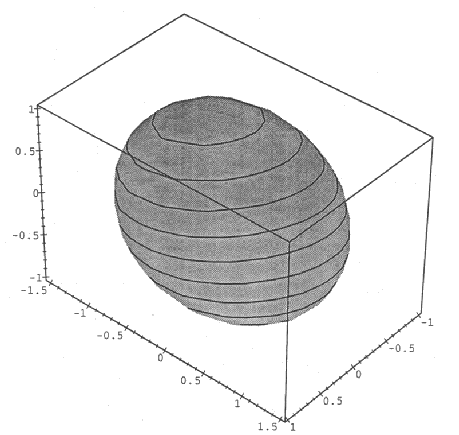
This Gabor model is a function defined in 3D spatiotemporal space and it is impossible to visualize (as it would require viewing in a 4D space). To compromise, we can let the function equal to a particular constant and to show the corresponding isosurface of the function in the 3D spatiotemporal space.