Representing Visual Motion in Spatiotemporal Space

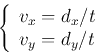
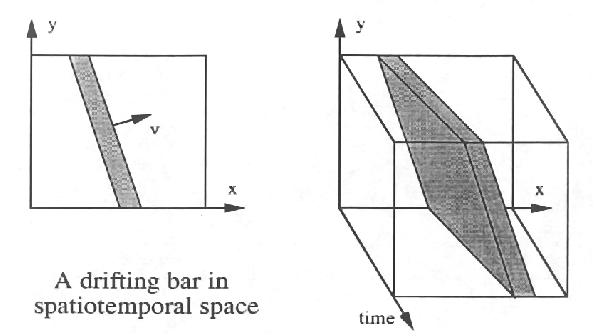
Visual motion is obviously a spatiotemporal process that takes place in time as well as in 2D space. A visual motion can be descirbe by the simple formula

$$\left\{ \begin{array}{l} v_x=d_x/t \\ v_y=d_y/t \end{array} \right.$$

where $(v_x, v_y)$ and $(d_x, d_y)$ are the speeds and the displacements in the $x$ and $y$ dimensions, respecitvely. These formulas can be written more concisely in vector form

$${\bf v}={\bf d}/t$$

where ${\bf d}=[d_x, d_y]$ is the displacement in the 2D space, and the velocity vector ${\bf v}=[v_x. v_u]=v \cdot {\bf v}/v$ represent both the speed $v$ and the direction ${\bf v}/v$ (a unit vector) of the motion. For example, a moving bar in the visual field can be represented in a 3D spatiotemporal space as shown below:

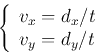
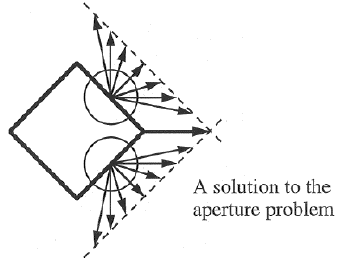
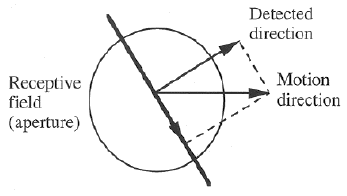
An important issue of visual motion detection is the aperture problem, as shown in the figure, which illustrates the fact that the true motion direction of a line feature can not be determined from inside the receptive field (aperture) of a cell. This is simply because any motion along the line is not detectable.

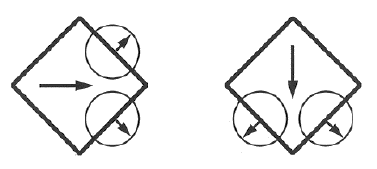
The figure below shows a simple mathematical solution to the aperture problem. However, this solution is not biologically plausible and is unlikely to resemble how the visual system solve the aperture problem. This issue will be discussed in the motion processing chapter.