


Next: Gabor model of V1
Up: The Primary Visual Cortex
Previous: Spatial Frequency Analysis -
Similar to the Gaussian model for the center-surround receptive field of the
retina ganglion cells, here we will develop a more comprehensive model for the
V1 cells that can account for multiple aspects of their response properties, such
as orientation selectivity, motion (direction and speed) selectivity, and frequency
responses in both spatial and temporal domains.
First, we consider the two components in the spatial aspect of the model:
- A Gassion function (used before for modeling the center-surround RF of the
retina ganglion cells) is used to model the spatially limited receptive field
of a V1 cell:
where
![${\bf r}=[x, y]$](img14.png) is a vector representing a position in the 2D visual
space,
is a vector representing a position in the 2D visual
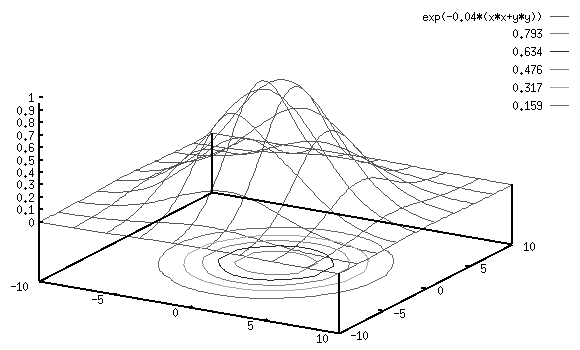
space, 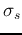 represents the size of the RF, and the subsript s is for space.
represents the size of the RF, and the subsript s is for space.
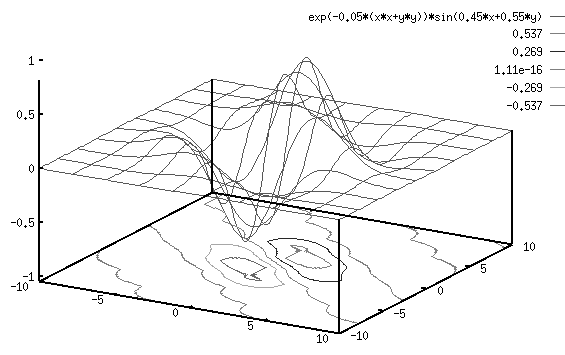
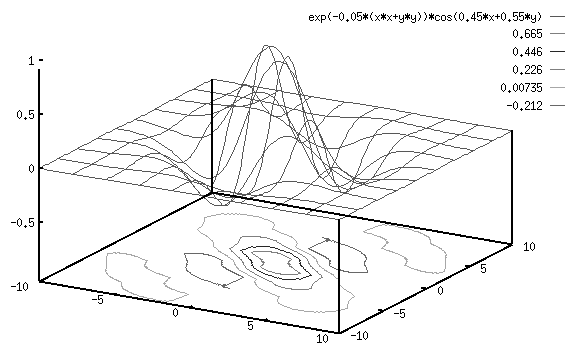
- A 2D sinusoidal function is used to model the V1 (simple) cells' receptive
field of certain orientations:
where 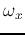 and
and 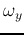 are the spatial frequencies in the x and y
directions, respectively,
are the spatial frequencies in the x and y
directions, respectively,
![${\bf\omega}_s=[\omega_x, \omega_y]$](img17.png) is a vector
representing the spatial frequency, and
is a vector
representing the spatial frequency, and 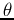 is a phase angle which
determines where in the elongated receptive field the
is a phase angle which
determines where in the elongated receptive field the 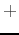 and
and 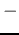 regions
are (responding to bright and dark stimuli, respectively).
regions
are (responding to bright and dark stimuli, respectively).
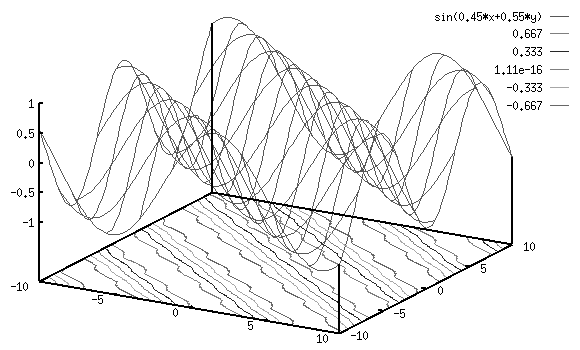
Note that the 2D spatial frequency vector
![${\bf\omega}_s=[\omega_x, \omega_y]$](img17.png) can be
expressed by its magnitude
can be
expressed by its magnitude 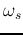 and direction n (a unit vector along the
direction):
and direction n (a unit vector along the
direction):
where
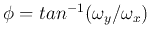 , and equivalently the two spatial frequency
components in
, and equivalently the two spatial frequency
components in 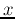 and
and 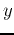 can be written as
can be written as
The product of the above two functions is a Gabel function which is used to
model the receptive field of a V1 cell:



Next: Gabor model of V1
Up: The Primary Visual Cortex
Previous: Spatial Frequency Analysis -
Ruye Wang
2013-04-08
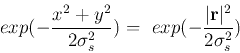


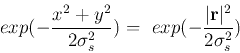


![]() can be
expressed by its magnitude
can be
expressed by its magnitude ![]() and direction n (a unit vector along the
direction):
and direction n (a unit vector along the
direction):
![\begin{displaymath}\left\{ \begin{array}{l} \omega_s=\sqrt{\omega_x^2+\omega_y^2...
...=[cos \mbox{ } \phi, sin \mbox{ } \phi]
\end{array} \right.
\end{displaymath}](img22.png)
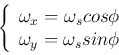
![\begin{displaymath}G(x,y)=exp(-\frac{ \vert {\bf r} \vert ^2 }{2\sigma_s^2} ) \mbox{ }
cos[( {\bf r} \cdot {\bf\omega}_s)+\theta]
\end{displaymath}](img25.png)

