


Next: Gaussian channel
Up: Neural Signaling III -
Previous: Neuronal response as a
- Conditional probabilities
Let A and B be two random events and P(A) and P(B) be their probabilities.
The probability of the joint event of both A and B, represented by P(A,B),
can be obtained as
P(A,B)=P(A) P(B/A)=P(B) P(A/B)
where P(A/B) is the conditional probability of event A given the condition that
event B, and P(B/A) is defined similarly.
If the two events are independent of each other, i.e., how likely event A will
occur is independent of whether event B occurs, and vice versa, then
and the joint probability becomes
P(A,B)=P(A) P(B)
- Stimuli and responses as random variables
The response property of a neuron can be characterized by the tuning curve
which represents how the neuron responds differently to stimulus with a varying
parameter. When there are two varying parameter, the tuning surface is used.
The shape of one dimensional tuning curves usually fall into one of two categories,
sigmoidal shaped, as the tuning for contrasts or near and far stereo cells for
distances, and bell shaped (Gaussian), as for orientation or direction of motion.
The a neuron is treated as a communication channel which receives the stimuli
s(t) as the input and generates the spike trains
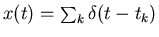 as
the output. Here both s(t) and x(t) are treated as random variables and the
observing x(t) as the response to s(t) is considered as a process in which
certain information (e.g., about the external world from the sensory stimuli) is
gained. To describe the relationship between them, that is, how the stimulus affects
the response and how the response reflects the stimulus, we define
as
the output. Here both s(t) and x(t) are treated as random variables and the
observing x(t) as the response to s(t) is considered as a process in which
certain information (e.g., about the external world from the sensory stimuli) is
gained. To describe the relationship between them, that is, how the stimulus affects
the response and how the response reflects the stimulus, we define
- p(s(t)), the probability distribution of s(t);
- p(x(t)), the probability distribution of x(t);
-
p[ x(t)/s(t) ], conditional probability of observing x(t) given the
condition of s(t). This describes how the information in the stimulus
is coded in the response of the neuron. The tuning curve is the result
of measuring this probability.
-
p[ s(t) / x(t) ], conditional probability of stimulus s(t) given the
observed x(t) as the condition. This is related to the inverse problem
of how to decode the response to get information about the stimulus.
These probabilities are all related to the joint probability of both s(t) and
x(t)
- Neuronal response as communication channel
p(s) is also called the a priori probability of input s, as it represents
the likelihood of s before the neuron responding to it; and p(s/x) is called
the post priori probability of s, as it represents the likelihood of s
given that the neuron has responded to it by of x. As observing x will always
more or less gain some information about s, we have
where the equal sign is for the worst case where x is completely irrelevant
to s therefore nothing about s can be learned from x.
The total information gained from this process is quantitatively given by
if the base of log is 2, then the unit of information is bit.
- Information I - ideal case
In the ideal case without noise, complete information about the stimuli can be
obtained in the sense that any given stimulus s is responded to with a specific
x, i.e,, p(s/x)=1,
Note that the less likely an event (small p(s)), the more information is
gained by learning this event occurs. (e.g., snow vs. fine whether in Los
Angeles.) In particular, if p(s)=1, no information is gained (I=0), due to
the log operation.
If the input is not a binary random event (either happens or not with probability
P), but a random variable of varying values s with probability distribution
p(s), then the information gained in an ideal communication channel is the
weighted average of information for all possible values of s:
if s is discrete, or
if s is continuous.
- Information II - with noise
If the system is noisy, the stimulus-response relationship is no longer definite,
as the same s may be responded to with different x due to noise, i.e.,
p(s/x) < 1. Here we first find the information about s gained when observing
a particular x:
Then we find the total information about s gained when observing all possible
x:
where
and
- Entropy
We define H(s) as the entropy of s. Note that as H(s) is the same as
the complete information gained in the ideal case, it represents the maximum
possible information available about s that can be gained. Since information
gaining can be considered the same process as uncertainty reduction, H(s) also
represents the uncertainty about s before observing x. And H(s/x) is the
conditional entropy, representing the uncertainty of s after observing
x. If the base of logarithm is 2, the unit of entropy is bit.
The information gained
I=H(s)-H(s/x) is thus called mutual information
and represents the uncertainty reduction from H(s) before observing x to
H(s/x) after observing x. In the ideal case p(s/x)=1, after observing s
the uncertainty becomes zero H(s/x)=0, and the complete information about s
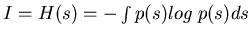 is gained.
is gained.
As an example, consider an experiment with n equally likely possible outcomes
si (
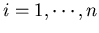 ). The probability for a particular si to occur is
p(si)=1/n. Now the total uncertainty, the entropy, of this experiment is
). The probability for a particular si to occur is
p(si)=1/n. Now the total uncertainty, the entropy, of this experiment is
We see that under the condition of equal likelihood, the entropy is simply the
logarithm of the total number of possible outcomes. If n=8, then the entropy,
i.e, the maximum possible information available about this experiment, is
log2 8=3 bits.
- Entropy under given conditions
Here we find the probability distribution p(x) to maximize the entropy
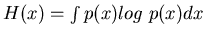 subject to some given conditions, as well as
subject to some given conditions, as well as
or
This kind of constrained optimization problem can be solved by Lagrange multiplier
method.
-
Given the range of a random variable
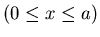 ,
the uniform distribution
,
the uniform distribution
has the maximum entropy
H(x)=log a
- Given the range of a random variable
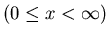 and its mean
and its mean 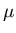 ,
the exponential decay distribution
,
the exponential decay distribution
has the maximum entropy
-
Given the variance
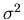 of a random variable x, we find the normal
(Gaussian) distribution
of a random variable x, we find the normal
(Gaussian) distribution
has the maximum entropy
The maximum entropy is proportional to
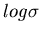 (independent of
(independent of 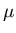 ).
).
Also as the variance 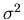 can be considered as the dynamic energy contained
in x, we see that among all possible distributions with the same uncertainty,
Gaussian distribution requires the minimum energy.
can be considered as the dynamic energy contained
in x, we see that among all possible distributions with the same uncertainty,
Gaussian distribution requires the minimum energy.
If the only knowledge about a random experiment is the mean 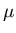 and variance
and variance
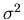 (which can be estimated by carrying the experiment a large number of
times), then its unknown probability distribution can be best estimated by a
normal distribution
(which can be estimated by carrying the experiment a large number of
times), then its unknown probability distribution can be best estimated by a
normal distribution
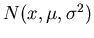 ,
as it imposes minimum artificial
constraint by allowing the maximum uncertainty.
,
as it imposes minimum artificial
constraint by allowing the maximum uncertainty.
- Entropy of spike trains
We now know that the amount of information available about the external world is
limited by the entropy of the input sensory signals. And, on the other hand,
how much information about the sensory input the spike trains can provide is
limited by the entropy of these spike trains, as considered below.
- Entropy of spike count
Here we ignore the temporal pattern of the spike trains and characterize each
spike train only by the total number of spikes n in a time window T. The range
of n is
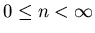 .
The mean of n is
.
The mean of n is
where r is the firing rate representing number of spikes per unit time (e.g.,
msec).
It can be shown that the distribution with maximum entropy is
where
and the maximum entropy is
Here the plot of p(n) is very similar to that of the
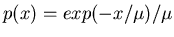 in the continuous case.
in the continuous case.
To find the entropy per unit time, we divide H(n) by T to obtain the
entropy rate (bit per second) representing amount of information gained
per unit time. Or, to find the information carried by each spike, we divide
H(n) by 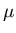 .
.
Shown in the plot is the plot of entropy per spike as a function of 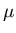 .
.
- Entropy of spike train
To compute the entropy without ignoring the temporal pattern of the spike train,
we divide the time window T into 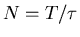 bins of width
bins of width 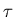 where
where 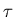 is
short to allow no more than one spike to fit in (but long enough so that a spike
never needs to take two bins time). Now each spike train can be represented by a
N-bit string of 0's and 1's. The number of 1's in the string is N1=rT, where
r is the firing rate, number of spikes per unit time). And the probability for
any bit to be 1 is p=N1/N.
is
short to allow no more than one spike to fit in (but long enough so that a spike
never needs to take two bins time). Now each spike train can be represented by a
N-bit string of 0's and 1's. The number of 1's in the string is N1=rT, where
r is the firing rate, number of spikes per unit time). And the probability for
any bit to be 1 is p=N1/N.
The total number of different equally likely patterns of the string is
(choosing N1 of N bins to be 1):
As we know the entropy of a random experiment is the logarithm of the total number
of equally likely outcomes, the entropy of the string is
To deal with the factorials, use Stirling's formula
or
With this approximation, the entropy can be simplified to
| H |
= |
-N [ log p +(1-p) log (1-p) ] |
|
| |
= |
![$\displaystyle -\frac{T}{\tau}[(r\tau)log (r\tau) +(1-r\tau) log (1-r\tau)]$](img73.gif) |
|
Again dividing H by T, we get the entropy rate, and dividing H by the
total number of spikes N1=rT, we get the information carried by each spike.
The plot shows this information per spike as a function of 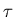 (with r=50/msec).
(with r=50/msec).
Comparing this plot with that of the spike count entropy, we see that each spike
now carry more information.
Conditional probabilities
Let A and B be two random events and P(A) and P(B) be their probabilities.
The probability of the joint event of both A and B, represented by P(A,B),
can be obtained as
P(A,B)=P(A) P(B/A)=P(B) P(A/B)
where P(A/B) is the conditional probability of event A given the condition that
event B, and P(B/A) is defined similarly.
If the two events are independent of each other, i.e., how likely event A will
occur is independent of whether event B occurs, and vice versa, then
and the joint probability becomes
P(A,B)=P(A) P(B)
Stimuli and responses as random variables
The response property of a neuron can be characterized by the tuning curve
which represents how the neuron responds differently to stimulus with a varying
parameter. When there are two varying parameter, the tuning surface is used.
The shape of one dimensional tuning curves usually fall into one of two categories,
sigmoidal shaped, as the tuning for contrasts or near and far stereo cells for
distances, and bell shaped (Gaussian), as for orientation or direction of motion.
The a neuron is treated as a communication channel which receives the stimuli
s(t) as the input and generates the spike trains
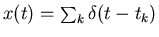 as
the output. Here both s(t) and x(t) are treated as random variables and the
observing x(t) as the response to s(t) is considered as a process in which
certain information (e.g., about the external world from the sensory stimuli) is
gained. To describe the relationship between them, that is, how the stimulus affects
the response and how the response reflects the stimulus, we define
as
the output. Here both s(t) and x(t) are treated as random variables and the
observing x(t) as the response to s(t) is considered as a process in which
certain information (e.g., about the external world from the sensory stimuli) is
gained. To describe the relationship between them, that is, how the stimulus affects
the response and how the response reflects the stimulus, we define
- p(s(t)), the probability distribution of s(t);
- p(x(t)), the probability distribution of x(t);
-
p[ x(t)/s(t) ], conditional probability of observing x(t) given the
condition of s(t). This describes how the information in the stimulus
is coded in the response of the neuron. The tuning curve is the result
of measuring this probability.
-
p[ s(t) / x(t) ], conditional probability of stimulus s(t) given the
observed x(t) as the condition. This is related to the inverse problem
of how to decode the response to get information about the stimulus.
These probabilities are all related to the joint probability of both s(t) and
x(t)
Neuronal response as communication channel
p(s) is also called the a priori probability of input s, as it represents
the likelihood of s before the neuron responding to it; and p(s/x) is called
the post priori probability of s, as it represents the likelihood of s
given that the neuron has responded to it by of x. As observing x will always
more or less gain some information about s, we have
where the equal sign is for the worst case where x is completely irrelevant
to s therefore nothing about s can be learned from x.
The total information gained from this process is quantitatively given by
if the base of log is 2, then the unit of information is bit.
Information I - ideal case
In the ideal case without noise, complete information about the stimuli can be
obtained in the sense that any given stimulus s is responded to with a specific
x, i.e,, p(s/x)=1,
Note that the less likely an event (small p(s)), the more information is
gained by learning this event occurs. (e.g., snow vs. fine whether in Los
Angeles.) In particular, if p(s)=1, no information is gained (I=0), due to
the log operation.
If the input is not a binary random event (either happens or not with probability
P), but a random variable of varying values s with probability distribution
p(s), then the information gained in an ideal communication channel is the
weighted average of information for all possible values of s:
if s is discrete, or
if s is continuous.
Information II - with noise
If the system is noisy, the stimulus-response relationship is no longer definite,
as the same s may be responded to with different x due to noise, i.e.,
p(s/x) < 1. Here we first find the information about s gained when observing
a particular x:
Then we find the total information about s gained when observing all possible
x:
where
and
Entropy
We define H(s) as the entropy of s. Note that as H(s) is the same as
the complete information gained in the ideal case, it represents the maximum
possible information available about s that can be gained. Since information
gaining can be considered the same process as uncertainty reduction, H(s) also
represents the uncertainty about s before observing x. And H(s/x) is the
conditional entropy, representing the uncertainty of s after observing
x. If the base of logarithm is 2, the unit of entropy is bit.
The information gained
I=H(s)-H(s/x) is thus called mutual information
and represents the uncertainty reduction from H(s) before observing x to
H(s/x) after observing x. In the ideal case p(s/x)=1, after observing s
the uncertainty becomes zero H(s/x)=0, and the complete information about s
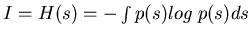 is gained.
is gained.
As an example, consider an experiment with n equally likely possible outcomes
si (
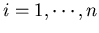 ). The probability for a particular si to occur is
p(si)=1/n. Now the total uncertainty, the entropy, of this experiment is
). The probability for a particular si to occur is
p(si)=1/n. Now the total uncertainty, the entropy, of this experiment is
We see that under the condition of equal likelihood, the entropy is simply the
logarithm of the total number of possible outcomes. If n=8, then the entropy,
i.e, the maximum possible information available about this experiment, is
log2 8=3 bits.
Entropy under given conditions
Here we find the probability distribution p(x) to maximize the entropy
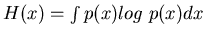 subject to some given conditions, as well as
subject to some given conditions, as well as
or
This kind of constrained optimization problem can be solved by Lagrange multiplier
method.
-
Given the range of a random variable
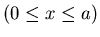 ,
the uniform distribution
,
the uniform distribution
has the maximum entropy
H(x)=log a
- Given the range of a random variable
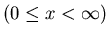 and its mean
and its mean 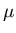 ,
the exponential decay distribution
,
the exponential decay distribution
has the maximum entropy
-
Given the variance
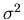 of a random variable x, we find the normal
(Gaussian) distribution
of a random variable x, we find the normal
(Gaussian) distribution
has the maximum entropy
The maximum entropy is proportional to
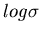 (independent of
(independent of 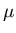 ).
).
Also as the variance 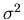 can be considered as the dynamic energy contained
in x, we see that among all possible distributions with the same uncertainty,
Gaussian distribution requires the minimum energy.
can be considered as the dynamic energy contained
in x, we see that among all possible distributions with the same uncertainty,
Gaussian distribution requires the minimum energy.
If the only knowledge about a random experiment is the mean 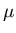 and variance
and variance
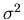 (which can be estimated by carrying the experiment a large number of
times), then its unknown probability distribution can be best estimated by a
normal distribution
(which can be estimated by carrying the experiment a large number of
times), then its unknown probability distribution can be best estimated by a
normal distribution
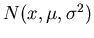 ,
as it imposes minimum artificial
constraint by allowing the maximum uncertainty.
,
as it imposes minimum artificial
constraint by allowing the maximum uncertainty.
Entropy of spike trains
We now know that the amount of information available about the external world is
limited by the entropy of the input sensory signals. And, on the other hand,
how much information about the sensory input the spike trains can provide is
limited by the entropy of these spike trains, as considered below.
- Entropy of spike count
Here we ignore the temporal pattern of the spike trains and characterize each
spike train only by the total number of spikes n in a time window T. The range
of n is
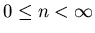 .
The mean of n is
.
The mean of n is
where r is the firing rate representing number of spikes per unit time (e.g.,
msec).
It can be shown that the distribution with maximum entropy is
where
and the maximum entropy is
Here the plot of p(n) is very similar to that of the
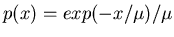 in the continuous case.
in the continuous case.
To find the entropy per unit time, we divide H(n) by T to obtain the
entropy rate (bit per second) representing amount of information gained
per unit time. Or, to find the information carried by each spike, we divide
H(n) by 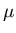 .
.
Shown in the plot is the plot of entropy per spike as a function of 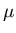 .
.
- Entropy of spike train
To compute the entropy without ignoring the temporal pattern of the spike train,
we divide the time window T into 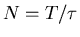 bins of width
bins of width 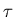 where
where 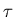 is
short to allow no more than one spike to fit in (but long enough so that a spike
never needs to take two bins time). Now each spike train can be represented by a
N-bit string of 0's and 1's. The number of 1's in the string is N1=rT, where
r is the firing rate, number of spikes per unit time). And the probability for
any bit to be 1 is p=N1/N.
is
short to allow no more than one spike to fit in (but long enough so that a spike
never needs to take two bins time). Now each spike train can be represented by a
N-bit string of 0's and 1's. The number of 1's in the string is N1=rT, where
r is the firing rate, number of spikes per unit time). And the probability for
any bit to be 1 is p=N1/N.
The total number of different equally likely patterns of the string is
(choosing N1 of N bins to be 1):
As we know the entropy of a random experiment is the logarithm of the total number
of equally likely outcomes, the entropy of the string is
To deal with the factorials, use Stirling's formula
or
With this approximation, the entropy can be simplified to
| H |
= |
-N [ log p +(1-p) log (1-p) ] |
|
| |
= |
![$\displaystyle -\frac{T}{\tau}[(r\tau)log (r\tau) +(1-r\tau) log (1-r\tau)]$](img73.gif) |
|
Again dividing H by T, we get the entropy rate, and dividing H by the
total number of spikes N1=rT, we get the information carried by each spike.
The plot shows this information per spike as a function of 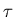 (with r=50/msec).
(with r=50/msec).
Comparing this plot with that of the spike count entropy, we see that each spike
now carry more information.



Next: Gaussian channel
Up: Neural Signaling III -
Previous: Neuronal response as a
Ruye Wang
1999-09-12
![]() as
the output. Here both s(t) and x(t) are treated as random variables and the
observing x(t) as the response to s(t) is considered as a process in which
certain information (e.g., about the external world from the sensory stimuli) is
gained. To describe the relationship between them, that is, how the stimulus affects
the response and how the response reflects the stimulus, we define
as
the output. Here both s(t) and x(t) are treated as random variables and the
observing x(t) as the response to s(t) is considered as a process in which
certain information (e.g., about the external world from the sensory stimuli) is
gained. To describe the relationship between them, that is, how the stimulus affects
the response and how the response reflects the stimulus, we define
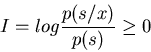
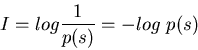
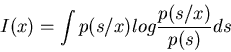
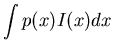
![$\displaystyle \int [ \int p(s/x) log \frac{p(s/x)}{p(s)} ds ] dx$](img39.gif)
![$\displaystyle \int p(x) [ \int p(s/x) log p(s/x) ds ] dx -\int p(x) [\int p(s/x) log p(s) ds] dx$](img40.gif)
![$\displaystyle \int p(x) [ \int p(s/x) log p(s/x) ds ] dx -\int [\int p(x) p(s/x) dx] log p(s) ds$](img41.gif)
![]() is gained.
is gained.
![]() ). The probability for a particular si to occur is
p(si)=1/n. Now the total uncertainty, the entropy, of this experiment is
). The probability for a particular si to occur is
p(si)=1/n. Now the total uncertainty, the entropy, of this experiment is
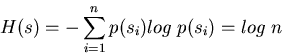
![]() subject to some given conditions, as well as
subject to some given conditions, as well as
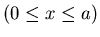 ,
the uniform distribution
,
the uniform distribution
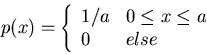
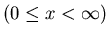 and its mean
and its mean 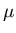 ,
the exponential decay distribution
,
the exponential decay distribution
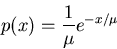
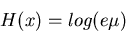
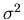 of a random variable x, we find the normal
(Gaussian) distribution
of a random variable x, we find the normal
(Gaussian) distribution
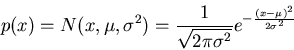
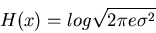
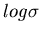 (independent of
(independent of 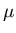 ).
).
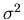 can be considered as the dynamic energy contained
in x, we see that among all possible distributions with the same uncertainty,
Gaussian distribution requires the minimum energy.
can be considered as the dynamic energy contained
in x, we see that among all possible distributions with the same uncertainty,
Gaussian distribution requires the minimum energy.
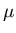 and variance
and variance
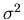 (which can be estimated by carrying the experiment a large number of
times), then its unknown probability distribution can be best estimated by a
normal distribution
(which can be estimated by carrying the experiment a large number of
times), then its unknown probability distribution can be best estimated by a
normal distribution
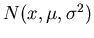 ,
as it imposes minimum artificial
constraint by allowing the maximum uncertainty.
,
as it imposes minimum artificial
constraint by allowing the maximum uncertainty.
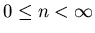 .
The mean of n is
.
The mean of n is
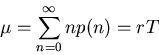
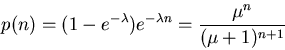
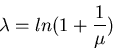
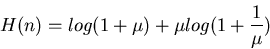
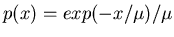 in the continuous case.
in the continuous case.
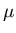 .
.
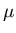 .
.
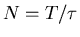 bins of width
bins of width 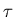 where
where 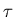 is
short to allow no more than one spike to fit in (but long enough so that a spike
never needs to take two bins time). Now each spike train can be represented by a
N-bit string of 0's and 1's. The number of 1's in the string is N1=rT, where
r is the firing rate, number of spikes per unit time). And the probability for
any bit to be 1 is p=N1/N.
is
short to allow no more than one spike to fit in (but long enough so that a spike
never needs to take two bins time). Now each spike train can be represented by a
N-bit string of 0's and 1's. The number of 1's in the string is N1=rT, where
r is the firing rate, number of spikes per unit time). And the probability for
any bit to be 1 is p=N1/N.
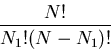
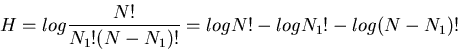
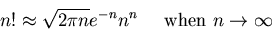
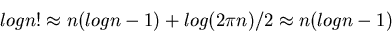
![$\displaystyle -\frac{T}{\tau}[(r\tau)log (r\tau) +(1-r\tau) log (1-r\tau)]$](img73.gif)
 (with r=50/msec).
(with r=50/msec).