A neuronal system can be approximated by a linear, time-invariant system (LTI)
with the relevant stimulus s(t) as the input and the observed spike train
x(t) as the output:
h(t) can be obtained experimentally by observing the spike train x(t) as
the response to the stimulus s(t) by
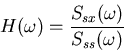
Specially if the stimulus is white or uncorrelated
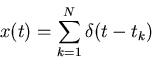
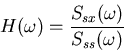
| h(t) | = | 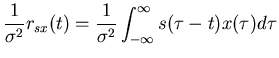 |
|
| = | 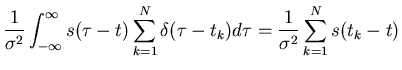 |
This is the reverse-correlation formula of h which states that the linear impulse response function of a neuron can be recovered by a simple spike-triggered average of the stimulus preceding the spikes.