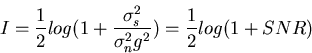Next: About this document ...
Up: Neural Signaling III -
Previous: Neural coding of information
Assume the stimulus is draw from a Gaussian distribution with variance
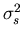 and the response is a linear function of the stimulus:
and the response is a linear function of the stimulus:
x=gs+n
where g is the gain and n is additive noise also normally distributed with
variance
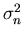 ,
then the mutual information gained by observing x is
,
then the mutual information gained by observing x is
where SNR is the signal-to-noise ratio defined as the signal variance to the
effective noise variance. If the stimulus is not Gaussian (but of the same
variance), according to the maximum entropy property of Gaussian, the mutual
information is less
Ruye Wang
1999-09-12
![]() and the response is a linear function of the stimulus:
and the response is a linear function of the stimulus: