Review of linear, time invariant system (LTI)

Neurons can be treated as linear encoding systems. Before further discussion, we first review the theory of linear, time invariant system (LTI).

• Response of a LTI system

  If a LTI system receives a signal x(t) as the input (stimulus), its output (response) y(t) can be found by this convolution operation:
  

  $$y(t)=h(t)*x(t)=\int_{t=-\infty}^{\infty} h(t-\tau)x(\tau)d\tau$$
  
  
  where h(t) is the impulse response function of the LTI system (also called the point spread function, Green's function). The Fourier transform of h(t) is called the transfer function of the neuron:
  
  $$H(\omega) = \cal{F} h(t) = \int_{t=-\infty}^{\infty} h(t) e^{-j\omega t} dt$$
  
  
  This LTI system can also be equivalently described in frequency domain as
  
  $$Y(\omega)=H(\omega)\; X(\omega)$$
  
  
  where $X(\omega)$, $Y(\omega)$, and $H(\omega)$ are the Fourier transforms of x(t), y(t) and h(t), respectively.

• Correlation and power spectrum

  The auto-correlation of a signal x(t) is defined as
  

  $$r_{xx}(t)=\int_{\tau=-\infty}^{\infty} x(\tau-t)x(\tau)d\tau$$
  
  
  Note that r_xx(t) is even symmetric
  
  r_xx(t)=r_xx(-t)
  
  
  The cross-correlation between two signals x(t) and y(t) is
  
  $$r_{xy}(t)=\int_{\tau=-\infty}^{\infty} x(\tau-t)y(\tau)d\tau$$
  
  
  The auto-correlation of a signal x(t) can be Fourier transformed to get its power spectrum
  
  $$S_{xx}(\omega)= \cal{F} r_{xx}(t) = \int_{t=-\infty}^{\infty} r_{xx}(t) e^{-j\omega t} dt$$
  
  
  and similarly for the cross-correlation of x(t) and y(t), their power spectrum is
  
  $$S_{xy}(\omega)= \cal{F} r_{xy}(t) = \int_{t=-\infty}^{\infty} r_{xy}(t) e^{-j\omega t} dt$$
  
  

• Obtain transfer function from power spectra

  The cross-correlation of the input x(t) and output y(t) of a LTI system can be obtained from the auto-correlation of the input and the impulse response h(t) of the system:
  

  $$\int_{\tau=-\infty}^{\infty} x(\tau-t)y(\tau)d\tau$$ r_xy(t) =

  $$\int_{\tau=-\infty}^{\infty} x(\tau-t) \int_{\tau=-\infty}^{\infty} x(\tau-t') h(t') dt' d\tau$$ =

  $$\int_{\tau=-\infty}^{\infty} h(t') \int_{\tau=-\infty}^{\infty} x(\tau-t) x(\tau-t') h(t') d\tau dt'$$ =

  $$\int_{\tau=-\infty}^{\infty} h(t') r_{xx}(t-t') dt'=h(t)*r_{xx}(t)$$ =

  
  
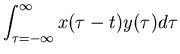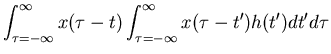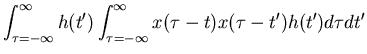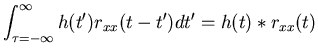  And similarly, the auto-correlation of the output can be obtained by
  

  $$\int_{\tau=-\infty}^{\infty} y(\tau-t)y(\tau)d\tau$$ r_yy(t) =

  $$\int_{\tau=-\infty}^{\infty} y(\tau-t) \int_{\tau=-\infty}^{\infty} x(\tau-t') h(t') dt' d\tau$$ =

  $$\int_{\tau=-\infty}^{\infty} h(t') \int_{\tau=-\infty}^{\infty} y(\tau-t) x(\tau-t') h(t') d\tau dt'$$ =

  $$\int_{\tau=-\infty}^{\infty} h(t') r_{xy}(t-t') dt'$$ =

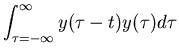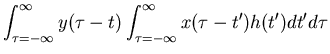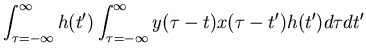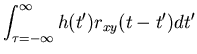  = h(t)*r_xy(t)= h(t)*h(t)*r_xx(t)

  
  

  These relations can be expressed in frequency domain as
  

  $$S_{xy}(\omega)=H(\omega) S_{xx}(\omega)$$
  
  
  and
  
  $$S_{yy}(\omega)=H(\omega) S_{xy}(\omega) H(\omega) S_{xx}(\omega) = \vert H(\omega) \vert^2 S_{xx}(\omega)$$