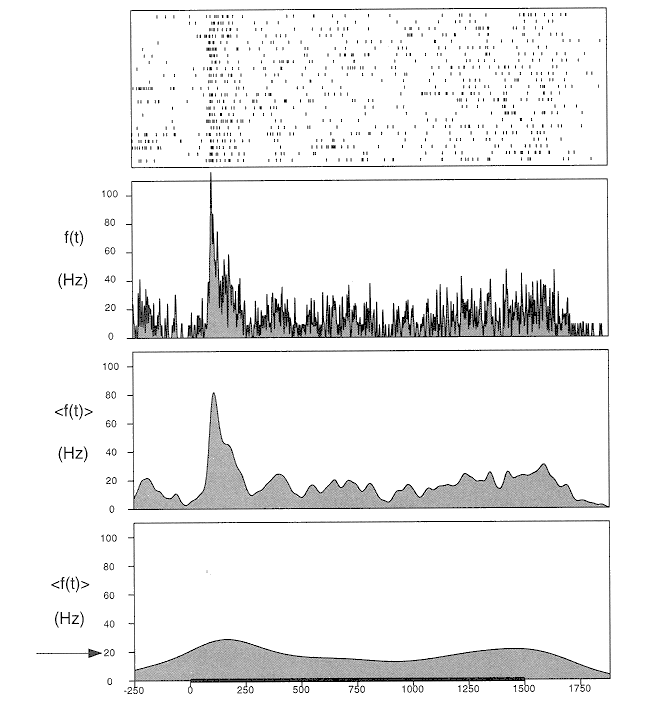
Neurons respond to external stimuli by generating a train of impulses (spikes)
of action potentials. In a typical physiological experiment, the same stimulus
is presented multiple times to a neuron and its response recorded (e.g., of 2
second long), as shown in the figure. The detailed compositions of the spike
trains vary from trial to trial. To characterize the response of the neuron to
the same stimulus, the average firing rate <f(t)> is computed by
averaging the responses of all trials over a brief time window ![]() of
a few msce. However, if the average time is too long, some details in the
neuronal signal may be averaged out and thereby some useful information may be
lost.
of
a few msce. However, if the average time is too long, some details in the
neuronal signal may be averaged out and thereby some useful information may be
lost.
To model the spike trains of the neuronal response, we first treat each spike
as a delta function:
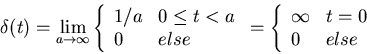
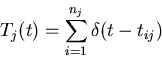
| <f(t)> | = | 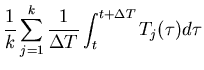 |
|
| = | 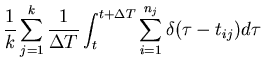 |
Alternatively, we can make the average more smooth over time by using a
Gaussian function
| <f(t)> | = | 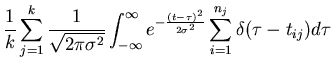 |