The Membrane Equation and Membrane Dynamics

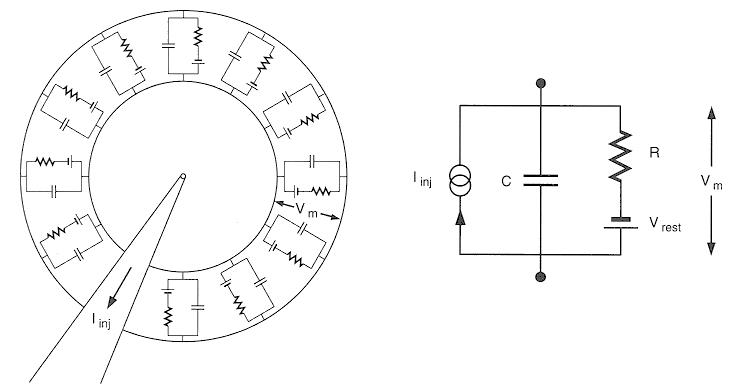
At the rest state, the ionic currents flowing through the ion channels balance each other to reach a dynamic equilibrium of zero net current, and the membrane potential as the voltage across the capacitor is the same as the rest potential of about 70 mV. But when there is an external current source as shown in the figure, either caused by a synaptic stimulus or injected from a intra-cellular microelectrode, the membrane potential will change as a function of time. According Kirchhoff's current law, the current source I_in is split into the current flowing through R and the current flowing through C:

$$I_{in}(t)=I_R(t)+I_C(t)=\frac{V_m(t)-V_{rest}}{R}+C\frac{dV_m(t)}{dt}$$

This is the membrane equation, which is a first order ordinary differential equation for the membrane potential V_m(t):

$$\tau \frac{dV_m(t)}{dt}+V_m(t)=V_{rest}+RI_{in}(t)$$

where $\tau=RC$ is the time constant of the membrane which is typically in the range of 10 msec. to 20 msec. Solving this membrane equation one can obtain the membrane potential as a function of time.

If we assume the external current source is a step function

$$I_{in}(t)=\left\{ \begin{array}{ll} 0 & t<0 \\ I_{in} & t \geq 0 \end{array} \right.$$

We assume the general solution of the membrane equation to be

$$V_m(t)=c_0 e^{-t/\tau}+c_1$$

from which we also get

$$\frac{dV_m(t)}{dt}=-\frac{c_0}{\tau}e^{-t/\tau}$$

where c₀, c₁ are two constants to be determined by the initial condition that the membrane potential is equal to the rest potential until the moment t=0 when the external current source is applied

V_m(0) = V_m(t=0) = V_rest

Substituting the general solution of V_m and dV_m/dt above into the membrane equation, we get

c₁=V_rest+RI_in

plugging this c₁ back to V_m, we get

$$V_m(t)=c_0e^{-t/\tau}+V_{rest}+RI_{in}$$

Applying the initial condition to this, we get

V_m(0)=c₀+V_rest+RI_in=V_rest

i.e.,

c₀=-RI_in

Now the special solution of V_m(t) can be obtained as

$$V_m(t)=RI_{in}(1-e^{-t/\tau})+V_{rest}$$

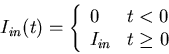
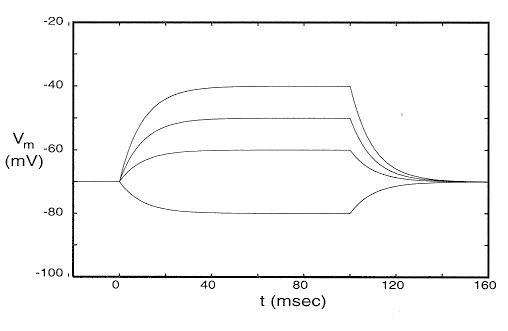
As shown in the figure, after the step current into the neuron, it will respond so that its membrane potential V_m(t) will either increased (more positive, or depolarized) or decreased (more negative, or hyperpolarized) depending on the direction of the external current source I_in. But this membrane potential change always has an exponential transition, instead of an instant response.