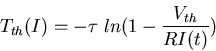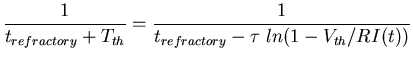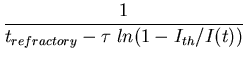Modeling a Spiking Neuron I - Integrate-and-Fire Model

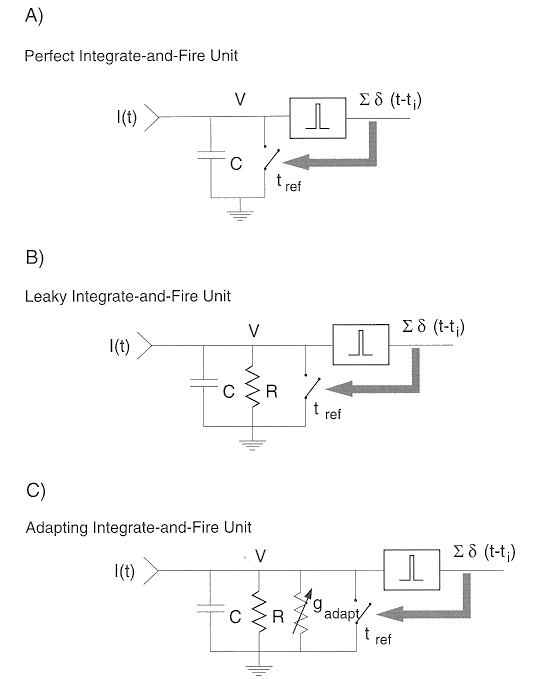
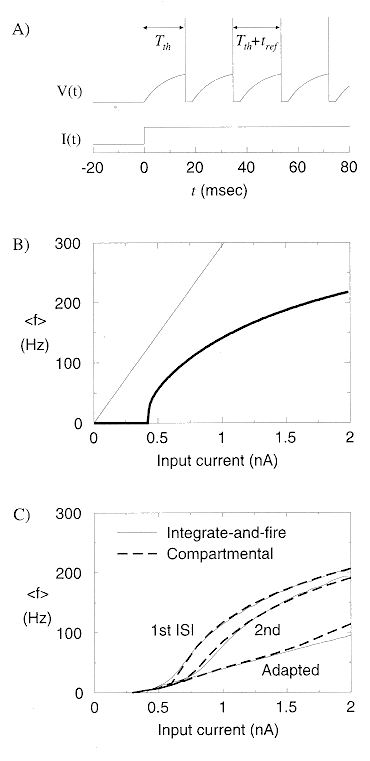
The generation of a spike train can be modeled by a integrate-and-fire circuit (also called voltage-threshold model) as shown in the figure. Note that case B is more realistic than case A as the resistor R is added to simulate the leakage through the membrane. The circuit is very similar to the electrical membrane model which is also charged by external current. The rectangle represents the spiking mechanism which generates a spike whenever the voltage across the RC component exceeds a threshold V_th, and at the same time the switch is momentarily closed to release all charge stored in C, and the next integration cycle begins and the circuit will be recharged.

The RC circuit in case (B) is described by this first order differential equation

$$C\frac{dV(t)}{dt}+\frac{V(t)}{R}=I(t)$$

To solve this equation for V(t), we again first assume the general solution

$$V(t)=c_0 e^{-t/\tau}+c_1$$

and find its derivative

$$\frac{dV(t)}{dt}=-\frac{c_0}{\tau} e^{-t/\tau}$$

Substituting them in the original equation, we have

$$-c_0e^{-t/\tau} + c_0e^{-t/\tau} + c_1=RI(t)$$

and get

c₁=RI(t)

We now further assume V(t)|_t=0=V(0)=V₀ (the initial condition, e.g. V₀=V_rest), we have

$$V(0)=c_0 e^{-0/\tau}+c_1=c_0+c_1=V_0$$

and find

c₀=V₀-c₁=V₀-RI(t)

Having found both c₀ and c₁, we can finally get the special solution

$$V(t)=(V_0-RI(t))e^{-t/\tau}+RI(t)=V_0e^{-t/\tau}+RI(t)(1-e^{-t/\tau})$$

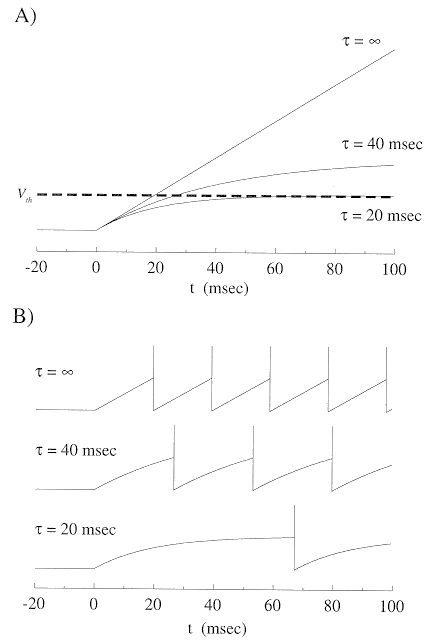
We see that V(t) can be considered as the combination of two independent processes, the discharge of C through the leakage of R from initial V₀ (the first term) and the recharge or discharge of C by I(t) (the second term). Whether I(t) will charge or discharge C depends on its direction, i.e., whether the neuron is excited or inhibited.

If we assume a constant external current I(t)=I, then V(t) will asymptotically approach a final value:

$$V(t)\vert _{t\rightarrow \infty}=RI$$

and the rate to reach the final value is

$$\frac{dV(t)}{dt}=\frac{RI}{\tau}e^{-t/\tau}=\frac{I}{C}e^{-t/RC}$$

For V(t) to reach the threshold V_th to trigger an action potential, we need

$$RI \ge V_{th}$$

i.e., the minimal sustained current is

I_th=V_th/R

Solving the above expression of V(t) (assuming V₀=0)

$$V(t)=RI(t)(1-e^{-t/\tau})$$

for t, and replacing V(t) by V_th, we find the time to trigger an action potential as a function of any external current I(t)>I_th:

$$T_{th}(I)=-\tau \; ln (1-\frac{V_{th}}{RI(t)})$$

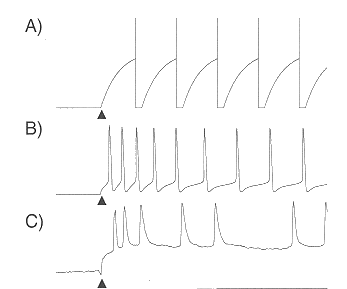
With a sustained external current, a spike train will be generated at the frequency

$$\frac{1}{t_{refractory}+T_{th}}=\frac{1}{t_{refractory}-\tau\; ln(1-V_{th}/RI(t))}$$ f =

$$\frac{1}{t_{refractory}-\tau\; ln(1-I_{th}/I(t))}$$ =

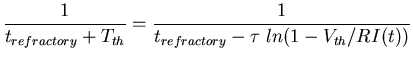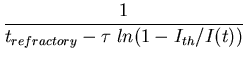where t_refractory is the refractory period. When I(t)<I_th, no spike is triggered. When I(t)>I_th, this equation relates the stimulus current I(t)and the firing rate f as shown in the f-I plot ( V_th=16mV, C=0.2nF, 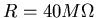$R=40 M\Omega$, t_refractory=3 msec). We see that the firing rate is a monotonic function of the external current I when I>I_th.

To summarize, we see that higher firing rate f may be caused by

• low threshold V_th;
• small refractory period t_refractory;
• large stimulus current I;
• large R (for high final voltage value);
• small C (for high charge rate dV(t)/dt).

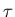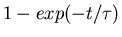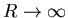Note here R plays double roles in the charging process. An increased R will increase $\tau$ and therefore slow down the growth of $1-exp(-t/\tau)$, but this is not dominant compared to the high final value also caused by increasing R. In the extreme case where $R \rightarrow \infty$ (the model becomes perfect or non-leaky), V(t) increases linearly at rate of I/C without bound and reaches V_th sooner than any 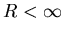$R<\infty$, as shown here: