Spatial Superposition of the Receptive Field

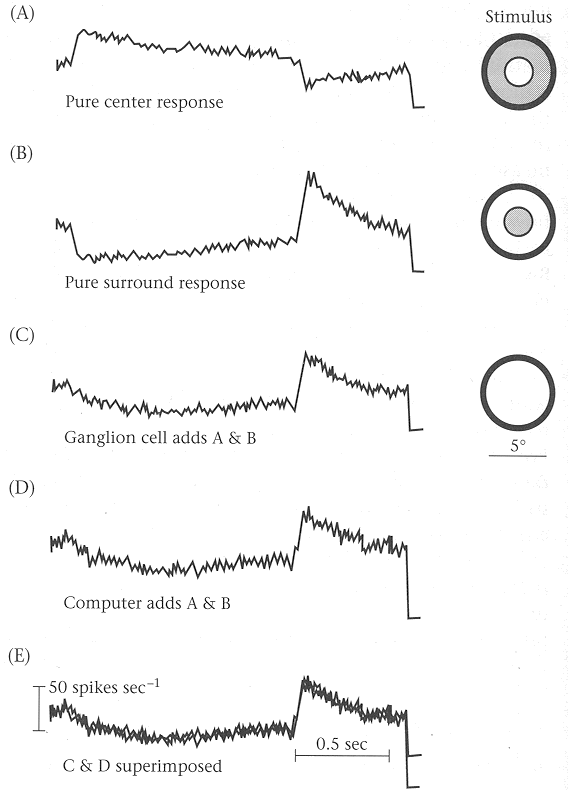
First we consider the superposition nature of the center and surround regions of the RF of a ganglion cell. It is shown by physiological studies that the linear sum of the response to a pure center stimulus and the response to a pure surround stimulus is a good prediction of the response to a stimulus covering both center and surround, such as the experiment by Enroth-Cugell and Pinto (1970) shown in this figure:

(A), (B) and (C) in the figure show, respectively, the average responses to a disk of light flashed in the RF center, an annulus flashed in the RF surround, and a disk of light covering the entire RF. (D) shows the superposition of (A) and (B), and (E) is a comparison of (C) and (D) which shows the superposition of responses in (A) and (B) is a good prediction of (C).

In fact, this supoerposition also holds in a more general sense than just for the center and surround. Consider a stimulus in an arbitrary position x=u, y=u inside the RF represented by $s(x,y,t)=\delta((x-u, y-v, t)$, and the corresponding response by h(t), the typical time response of, say, a midget ganglion cell. Here h(t) has both transient and sustained parts is not dependent on the spatial location (x_o, y_o). Now this stimulus-response relationship can be represented by

$$r(t)=T[ s(x,y,t) ]=T[ \delta(x-u, y-v) ]=h(t)$$

The stimilus to the overall RF s(x,y) can be considered as composed of many such local lights each with its own magnitude and time course:

$$s(x,y,t)=\int \int s(u,v,t) \delta(x-u, y-v, t) dx dy$$

The response of the cell to this signal will then be

$$T[ s(x,y,t)]=T[\int \int s(u,v,t) \delta(x-u, y-v, t) dx dy]$$ r(t) =

$$\int \int s(u,v,t) T[\delta(x-u, y-v, t)] dx dy=\int \int s(u,v,t) h(t) dx dy$$ =