Sampling and Aliasing

The image formed on the retina can be considered as a continuous 2D spatial function s(x,y), which is detected by the discrete individual receptors on the retina. In other words, the outputs of the retina to the brain are the spatial samples of this continuous function, due to the finite resolution of these receptors. There are about 25,000 cones in the 400 $\mu m$ diameter fovea area. Assuming the circular foveal area can be filled with circular receptors with diameter of $d \mbox{ } \mu m$, we have

$$\pi (400/2)^2 = 25,000 \pi (d/2)^2$$

Solving this equation we get $d \approx 2.5 \mu m$, which is also the distance between two neighboring receptors.

According to the sampling theorm based on Fourier theory, the sampling rate has to be higher than two times the highest frequency component in the signal (the Nyquist frequency) in order for the sampling system to detect (and possibly reconstruct) the signal without distortion or aliasing. If the signal to be sampled is a pure sinusoid, then the sampling theorem requires more than 2 samples per cycle of the sinusoid. Note that sampling rate is the reciprocal of the sampling period (interval between two neighboring samples) and vice versa.

As the sampling period of the fovea is about 2.5 $\mu m$, we know that the finest sinusoid the eye can distinguish has approximately 5 $\mu m$ cycle on the retina. Since one degree visual angle corresponds to 300 $\mu m$ distance on the retina, the highest spatial frequency the eye can detect is about 60 cycle/degree, or 1 cycle per minute. This theoretical upper limit of spatial resolution of the human eye happens to be also the upper limit of spatial resolution of the optics of the human eye. In other words, the optics of the eye matches the sampling capability of the retina, or vice versa.

When the spatial frequency of the scene is higher than this upper limit of 60 cycle/degree, aliasing will occur and a frequency lower than the real one will be perceived.

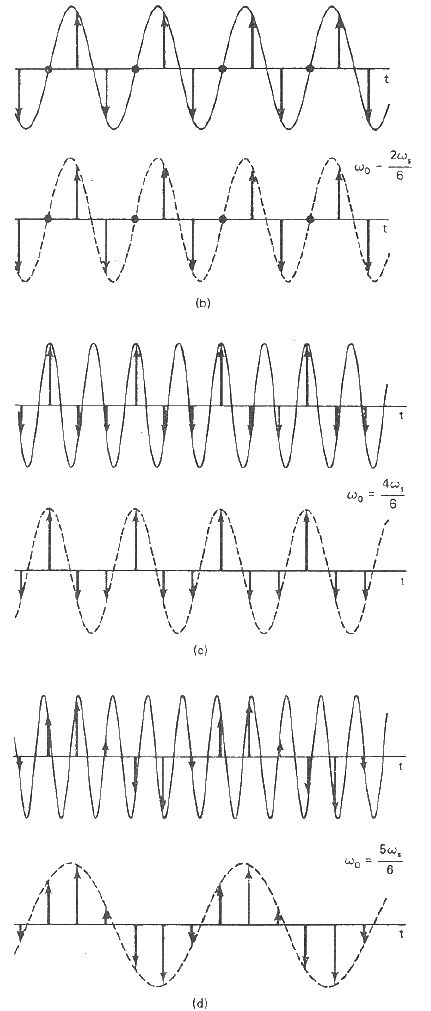
Thress different cases are shown in this figure. In (b) the sampling rate is higher than twice the signal frequency (the Nyquist frequency) and the original signal can be correctly recovered. However, in (c) and (d), the sampling rate is lower than twice the signal frequency and the recovered frequency is lower than the real signal frequency, the aliasing occurs.

To better understand the sampling theorem, try this web demo