Spatial Filtering

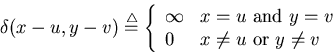
Some physiological studies on both vertebrates and invertebrates indicate that there exist lateral electrical connections between neighboring photoreceptors. It has been found that a significant percentage of response of a rod is due to its input from adjacent rods in addition to the light it absorbs.

If we denote the light spot at a spatial location (u, v) by a spatial delta function

$$\delta(x-u, y-v)\stackrel{\triangle}{=}\left\{ \begin{array}{... ... 0 & \mbox{$x\neq u$\space or $y\neq v$ } \end{array} \right.$$

then an arbitrary incoming visual scene can be considered as a spatial signal represented as the supurposition of many lights spots $s(u,v) \delta(x-u, y-v)$of spatial location (u, v) and intensity (e.g., amount of photons) s(u,v)

$$s(x,y)=\int \int s(u,v) \delta(x-u, y-v) du dv$$

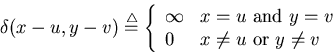
The response of a population of neighboring neurons to a light spot $\delta(x-u, y-v)$can also be represented as a spatial function g(x-u, y-v) which is no longer a localized delta function as it contains contribution from not only the receptor at the particular location of the light spot, but also its neighbors due to the lateral connections. We denote this population response as

$$g(x-u, y-v)=T[ \delta(x-u, y-v)]$$

Assuming linearity, the response of these neurons to a general spatial signal s(x,y) can be found as

$$T[s(x,y)]=T[\int \int s(u,v) \delta(x-u, y-v) du dv]$$ r(x,y) =

$$\int \int s(u,v) T[\delta(x-u, y-v)] du dv$$ =

$$\int \int s(u,v) g(x-u, y-v)] du dv$$ =

$$\stackrel{\triangle}{=}$$ s(x,y)*g(x,y)

Similar to the temporal filtering process, here the spatial response of the receptors is the convolution of the input signal s(x,y) and the point-spread function g(x,y), which has the similar smoothing effect in space so that the usual high spatial frequency random noise caused by quantum flucturation is attenuated.