Temporal Filtering

Above the threshold, the photoreceptors can be approximated as linear systems that convert light signal (photon streams) as input into neural response as output (depolarization or hyperpolarization of membrane potentials, change of neural transmitter release, and firing rates). This process can be in general modeled by

r(t)=T[ s(t) ]

where s(t) is the light input as function in time and r(t) is the response output also as function of time. By definition, a linear system's response to the weighted sum of two stimuli is equal to the weighted sum of its responses to the two stimuli individually:

T[c₁ s₁ + c₂ s₂]=c₁ T[s₁] + c₂ T[s₂]

and in general

$$T[\sum_i c_i s_i]=\sum_i c_i T[s_i]$$

Upon capturing a single photon at time instance $t=\tau$ represented by a delta function

$$\delta(t-\tau)\stackrel{\triangle}{=}\left\{ \begin{array}{ll} \infty & t=\tau \\ 0 & t\neq \tau \end{array} \right.$$

a photoreceptor responds with $h(t-\tau)$, a gradually increasing and then decreasing polarization change which lasts several milliseconds:

$$r(t)=T[ s(t) ]=T[ \delta(t-\tau) ]=h(t-\tau)$$

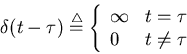
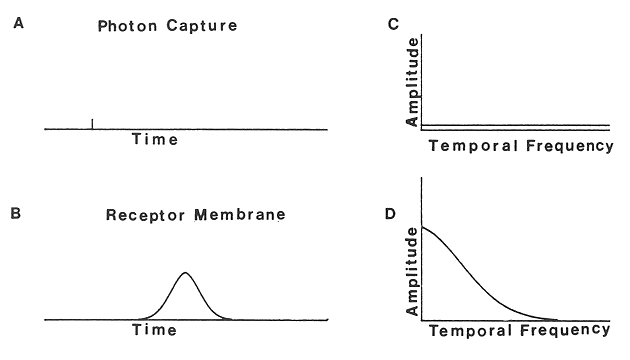
The receptor is assumed to be a linear system in the sense that its response to n photons all captured at $t=\tau$ is $n h(\tau)$.

In general, if in the photon stream of light there are $s(\tau)$ photons captured in time interval $\tau < t <\tau+\Delta$, the light can be represented as a time signal

$$s(t)=\sum_\tau s(\tau) \delta(t-\tau)$$

here the summation is over all $\tau=k \Delta$, where $k=\cdots, -2, -1, 0, 1, 2, \cdots$. The response of a receptor to this signal is

$$T[ s(t)]=T[\sum_\tau s(\tau) \delta(t-\tau)]$$ r(t) =

$$\sum_\tau s(\tau) T[\delta(t-\tau)]=\sum_\tau s(\tau) h(t-\tau)$$ =

$$\stackrel{\triangle}{=}$$ s(t)*h(t)

Now if we let $\Delta \rightarrow 0$, the input light signal becomes

$$s(t)=\int s(\tau) \delta(t-\tau) d\tau$$

and the response becomes

$$r(t)=\int s(\tau) h(t-\tau) d\tau$$

This is called the convolution of s(t) and h(t). In general, convolution describes the input-output relationship of a system if it is linear and time-invariant (LTI), and its response to a impulse $\delta(t)$ is h(t), called impulse response function (also called point spread function (PSF) and Green's function in physics).

The convolution of light signal x(t) with the impulse response function h(t)of the photoreceptors has the effect of smoothing (low-pass filtering) the input signal. When the signal is weak and affected by random fluctuation caused by the probabilistic nature of photon capture, the light signal x(t) may have random high frequency noise superimposed on the real signal which usually changes slowly. The smoothing effect will remove this type of noise while reserving the slowly changing component of the signal.