


Next: Spatiotemporal energy based motion
Up: The Models
Previous: Correlation based motion detection
The visual signal form on the retina can be treated as a two-dimensional
time-varying brightness function
I(x(t), y(t), t). If this function is moving
with a local velocity
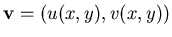 ,
where u and v are the
velocity components in the x and y directions, respectively, then the
brightness at point
,
where u and v are the
velocity components in the x and y directions, respectively, then the
brightness at point
![$[x(t+\delta t),y(t+\delta t)]=[x+u \delta t, y+v \delta t]$](img29.gif) at
time
at
time
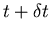 is approximately the same as the brightness at point
[x,y] at time t (assuming the luminance of the 3D point has changed very
little by the displacement due to motion), i.e.,
is approximately the same as the brightness at point
[x,y] at time t (assuming the luminance of the 3D point has changed very
little by the displacement due to motion), i.e.,
In order to estimate the velocity u(x,y) and v(x,y), the left-hand side
of this equation can be expanded into Taylor series with respect to time and
the equation becomes:
where 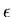 represents the second and higher terms of
represents the second and higher terms of 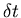 in the
expansion. When
in the
expansion. When 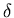 approaches 0, this error
approaches 0, this error 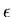 quickly disappears
and the optic flow constraint equation can be obtained:
quickly disappears
and the optic flow constraint equation can be obtained:
where Ix, Iy, and It represent the partial derivatives of I(x,y,t)with respect to variables x, y and t, respectively, 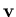 is the
2D velocity
is the
2D velocity
and
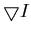 is the gradient (a vector) of I(x,y):
is the gradient (a vector) of I(x,y):
with
 being the gradient operator:
being the gradient operator:
The above equation, called the optic flow constraint equation, can be
rewritten as
which indicates that the rate of temporal change in intensity of the scene
is the dot product of its rate of spatial change and its motion velocity.
As this equation has two independent unknowns u and v, the problem is
ill-posed in the sense that it does not have a unique solution. In order to
obtain a unique solution, additional condition needs to be imposed.
- First, the aperture problem can be used as such a condition.
Aperture problem is encountered by any visual system (artificial or biological)
based on an array of sensors with limited ``aperture'' (receptive field for
neurons). Under this constraint, each sensor can only see a small local area
(represented by the circles in the figure) and detect the component velocity
perpendicular to the most salient line feature inside the aperture, such as a
piece of edge, or boundary, etc., instead of the true 2D motion. The normal
direction of such an orientational feature can be found as the gradient of the
brightness
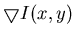 (along this direction the brightness
changes most quickly), and an additional equation requiring the velocity
(along this direction the brightness
changes most quickly), and an additional equation requiring the velocity
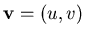 to be in the same direction as the gradient can be added
to be in the same direction as the gradient can be added
Now the velocity (u,v) satisfying both this constraining condition and
the optic flow constraint equation obtained previously can be uniquely found
to be
The component of optical flow in the direction of the brightness gradient is
- Alternatively, the ill-posed problem can be solved using a so-called
regularization methods that imposes a smoothness condition on the velocity.
This method minimizes the error in the optic flow constraint equation over
the entire visual field
under the condition that the velocity (u,v) should be as smooth as
possible, i.e., the magnitudes of the velocity gradients (representing
local spatial changes of the velocity) should be minimized:
This is a problem in the calculus of variations and the associated
Euler-Lagrange equations are
where
is the Laplacian operator. This pair of partial differential equations can be
solved numerically using iterative methods.
This gradient method for detecting motion seems very mathematically involved.
However, a network implementation of this method was developed in
[16] which is more biologically plausible.
In discrete case all spatial functions are represented by 2D arrays and all
spatial partial derivatives are replaced by differences between neighboring
elements. And the smoothness condition becomes the mininization of the
following
and the optic flow constraint requires the minimization of the following
Put the smoothness condition and optic flow constraint together, we want
to find uk,l's and vk,l's that minimize
where 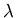 is a parameter for adjusting the relative importance of the
two terms. To do so, we set the partial derivatives of e with respect to
uk,l and vk,l to zero:
is a parameter for adjusting the relative importance of the
two terms. To do so, we set the partial derivatives of e with respect to
uk,l and vk,l to zero:
where
can be considered as the local average of ui,j. Note that the constant
coefficients 2 and 4 can be dropped due to the arbitrary 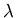 ,
and the
second equation above can be treated in exactly the same way. Now we can get
,
and the
second equation above can be treated in exactly the same way. Now we can get
This linear equation system of two equations and two unknowns can be solved to get
This can be readily implemented by an iterative algorithm (Gauss-Seidel method):
where
There are two major problems associated with this gradient based method. First,
the method relies on the image gradient
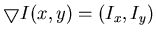 assumed
to be available at every location of the scene. But in fact gradient is not available
(zero gradient) at all homogeneous regions of the image. A possible solution is to
interpolate from gradients of neighboring regions. Second, the smoothness condition
assumes local motion velocities are similar to each other, therefore causing
inaccuracy at all motion discontinuities (boundaries of moving objects). One
solution is to only smooth the motion velocities along the tangents of the image
discontinuities ( boundaries) but not accross (gradient).
assumed
to be available at every location of the scene. But in fact gradient is not available
(zero gradient) at all homogeneous regions of the image. A possible solution is to
interpolate from gradients of neighboring regions. Second, the smoothness condition
assumes local motion velocities are similar to each other, therefore causing
inaccuracy at all motion discontinuities (boundaries of moving objects). One
solution is to only smooth the motion velocities along the tangents of the image
discontinuities ( boundaries) but not accross (gradient).



Next: Spatiotemporal energy based motion
Up: The Models
Previous: Correlation based motion detection
Ruye Wang
2000-04-25
![]() ,
where u and v are the
velocity components in the x and y directions, respectively, then the
brightness at point
,
where u and v are the
velocity components in the x and y directions, respectively, then the
brightness at point
![]() at
time
at
time
![]() is approximately the same as the brightness at point
[x,y] at time t (assuming the luminance of the 3D point has changed very
little by the displacement due to motion), i.e.,
is approximately the same as the brightness at point
[x,y] at time t (assuming the luminance of the 3D point has changed very
little by the displacement due to motion), i.e.,
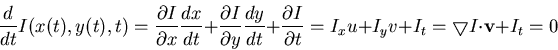
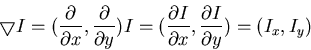
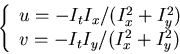
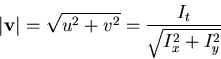
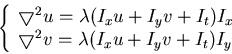
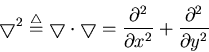
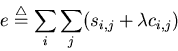
![]() is a parameter for adjusting the relative importance of the
two terms. To do so, we set the partial derivatives of e with respect to
uk,l and vk,l to zero:
is a parameter for adjusting the relative importance of the
two terms. To do so, we set the partial derivatives of e with respect to
uk,l and vk,l to zero:
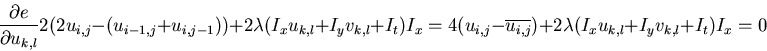
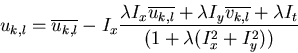
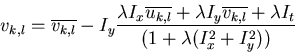
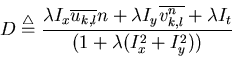
![]() assumed
to be available at every location of the scene. But in fact gradient is not available
(zero gradient) at all homogeneous regions of the image. A possible solution is to
interpolate from gradients of neighboring regions. Second, the smoothness condition
assumes local motion velocities are similar to each other, therefore causing
inaccuracy at all motion discontinuities (boundaries of moving objects). One
solution is to only smooth the motion velocities along the tangents of the image
discontinuities ( boundaries) but not accross (gradient).
assumed
to be available at every location of the scene. But in fact gradient is not available
(zero gradient) at all homogeneous regions of the image. A possible solution is to
interpolate from gradients of neighboring regions. Second, the smoothness condition
assumes local motion velocities are similar to each other, therefore causing
inaccuracy at all motion discontinuities (boundaries of moving objects). One
solution is to only smooth the motion velocities along the tangents of the image
discontinuities ( boundaries) but not accross (gradient).