


Next: Balancing the competition
Up: Appendix
Previous: Appendix
First, the net input of the jth node can be written in vector form:
where
![$W_j^T=[\cdots, w_{ij}, \cdots]$](img114.gif) and
and
![$X^T=[\cdots, x_i, \cdots]$](img115.gif) are
the input vector and weight vector of the jth node, respectively.
are
the input vector and weight vector of the jth node, respectively.
For each input pattern presented to the input layer, all output nodes compete
in a winner-take-all fashion. The node receiving the highest net input becomes
the winner and its output is set to a maximum value (typically 1), while the
outputs of the remaining nodes are set to a minimum value (typically 0) and
their weights are not changed.
The learning law for modifying the weights is:
where
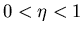 is the learning rate, zj=1 if Ni is a winner and
zj=0 otherwise. In order words, only the winner gets to modify its weights.
Learning process can be illustrated as in Fig. 10, where the
spheres represent the high dimensional feature space, dots and crosses are the
input patterns and weights, both represented as vectors in the feature space.
In the training process, each weight vector moves gradually from its initial
random position to the center of a cluster of similar input patterns. The
training terminates when the network reaches stable state where each
cluster of input patterns is represented by a unique output node, as shown in
Fig. 10(b). In other words, the weight vector W of a node is
approximately in the same direction as the average X of the input patterns
in the cluster represented by the node, i.e., W is proportional to X:
is the learning rate, zj=1 if Ni is a winner and
zj=0 otherwise. In order words, only the winner gets to modify its weights.
Learning process can be illustrated as in Fig. 10, where the
spheres represent the high dimensional feature space, dots and crosses are the
input patterns and weights, both represented as vectors in the feature space.
In the training process, each weight vector moves gradually from its initial
random position to the center of a cluster of similar input patterns. The
training terminates when the network reaches stable state where each
cluster of input patterns is represented by a unique output node, as shown in
Fig. 10(b). In other words, the weight vector W of a node is
approximately in the same direction as the average X of the input patterns
in the cluster represented by the node, i.e., W is proportional to X:
Figure 10:
The feature space before (a) and after (b) competitive learning
|



Next: Balancing the competition
Up: Appendix
Previous: Appendix
Ruye Wang
2000-04-25