


Next: About this document ...
Up: Appendix
Previous: Competitive learning
If the input patterns form a continuum instead of a set of nicely separable
clusters (as in the case of the network models for both MT and MST),
no obvious boundaries can be found to partition the feature space. In this
case, the results of competitive learning may be very different, anywhere
between two extremes: (a) the continuum of input patterns may be divided
relatively evenly, but randomly, into a set of clusters, each represented by
a particular output node, or (b) the entire continuum is represented by one
output node and all other nodes become dead nodes and never turn on.
To achieve the preferred result of (a), the competitive learning can be
modified to ensure some winning chance for every node. We can include a bias
term while computing the output of each node during competition:
Specifically, the bias term can be set to ([75])
where 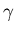 is a constant factor, n is the total number of nodes in the
competition, and fj is the frequency of winning for node Nj. Since bjis proportional to the difference between the equal winning probability 1/n
and the actual winning frequency fj, it has the tendency to make winning
harder for the frequent winners and easier for the frequent losers. Thus a
more balanced competition can be achieved.
is a constant factor, n is the total number of nodes in the
competition, and fj is the frequency of winning for node Nj. Since bjis proportional to the difference between the equal winning probability 1/n
and the actual winning frequency fj, it has the tendency to make winning
harder for the frequent winners and easier for the frequent losers. Thus a
more balanced competition can be achieved.



Next: About this document ...
Up: Appendix
Previous: Competitive learning
Ruye Wang
2000-04-25