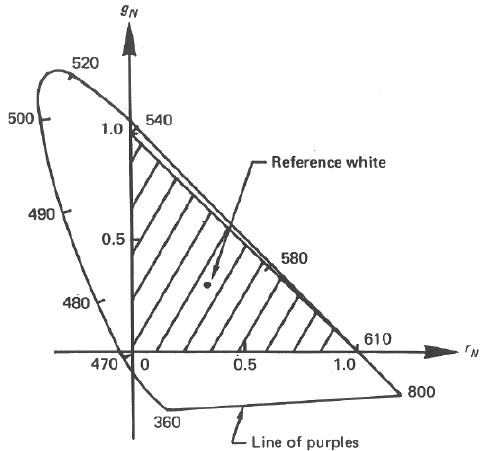
The colors on TV and computer screens are produced by three types of phosphors coated on the inner surface of the screen each activated by an electronic beam. When activated by the electronic beam, the phosphors emit respectively red, green, and blue light with certain spectral distributions and with intensity proportional to the current. By mixing these three colors as the primaries with different proportions, many other colors can be produced. These three primaries can be used as the basis functions in the color space as shown. As these primaries are real and actually implemented, the positive parts of their corresponding axes must lie entirely inside the conical solid representing all visible colors. In other words, the colors producible by the phosphors are only a subset of all visible colors. In the figure, the NTSC (National Television Systems Committee) receiver primaries are shown.

Any color inside the shaded triangle area can be generated by mixing the R, G, and B primaries at proper proportion. But as can be seen, certain perceivable colors outside the triangle cannot be generated by mixing the primaries.

This diagram shows some mixtures of the three primaries:
Question:
Is it possible to construct a set of three realizable primaries which can be used to match all perceivable colors with positive tristimulus values (weights)?
Answer:
Any set of three primaries is always represented by some three straight lines in the 3D color space, and all colors matchable by these primaries are inside the subspace spanned by the positive part of the three straight lines. But, on the other hand, all perceivable colors are inside the conical solid with curved surface (the spectrum locus and the purple line) which cannot be fit precisely by any three straight lines. As the result, we can either try to find a set of primaries with the positive part of the corresponding straight lines completely inside the conical solid, but still covering as much space as possible (such as the RGB primaries used for color screens) to make sure positive weights; or use a set of unrealizable primaries which can lie outside the conical solid so that the solid can be enclosed completely in the space spanned by the positive part of the corresponding straight lines, such as the CIE XYZ primaries. In other words, it is impossible to match all perceivable colors by a set of realizable primaries.