CIE's XYZ Coordinate System

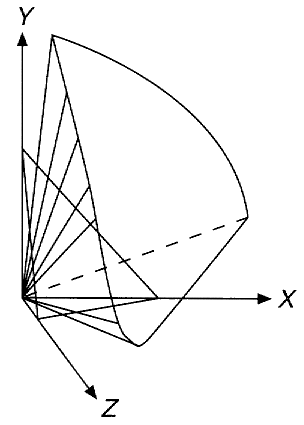
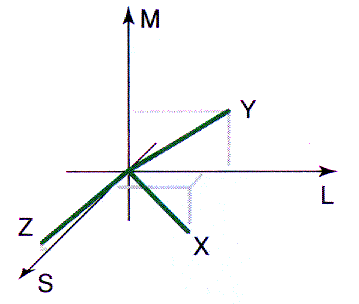
CIE developed a set of three hypothetical (unreal, imaginary) primaries X, Y, and Z in order to be able to match any color $L$ by mixing these primaries with positive weights $X(L)$, $Y(L)$ and $Z(L)$. This means that in the color space the three axes of X, Y and Z must lie outside the conical solid first discussed in the LMS coordinate system. (Or, equivalently the conical solid must lie entirely inside the positive octant of the XYZ coordinate system.) The XYZ primaries are not real because they cannot be physically realized. Otherwise some ``colors'' outside the conical solid might be produced by mixing the XYZ primaries with certain (positive) weights, a result directly contradicting the fact that all colors we can possibly see are inside the conical solid.

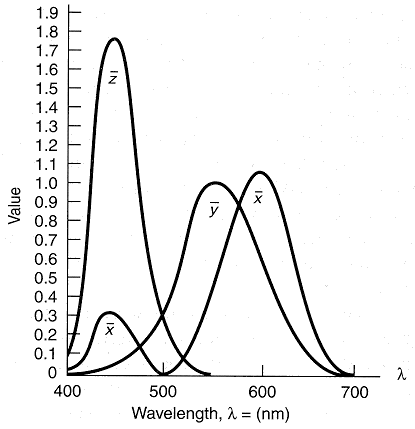
The tristimulus spectral matching curves for these XYZ primaries are shown in the figure, and indeed they are always positive for the entire range of visible wavelengths (and therefore all linear combinations thereof).

The chromaticity values of a color is defined by its weights for the three primaries normalized by the total energy $X+Y+Z$:

$$x=\frac{X}{X+Y+Z},\;\;y=\frac{Y}{X+Y+Z},\;\;z=\frac{Z}{X+Y+Z}$$

so that

$$x+y+z=1$$

Chromaticity values depend on the hue and saturation of the color, but are independent of the intensity. (Hue, saturation and intensity are three independent variables describing a color, as to be discussed later.)

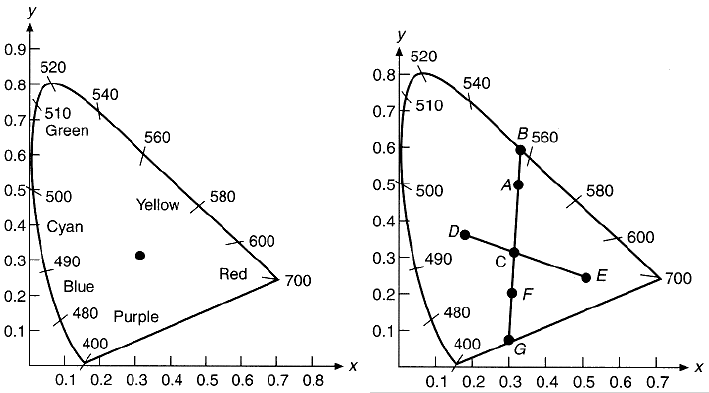
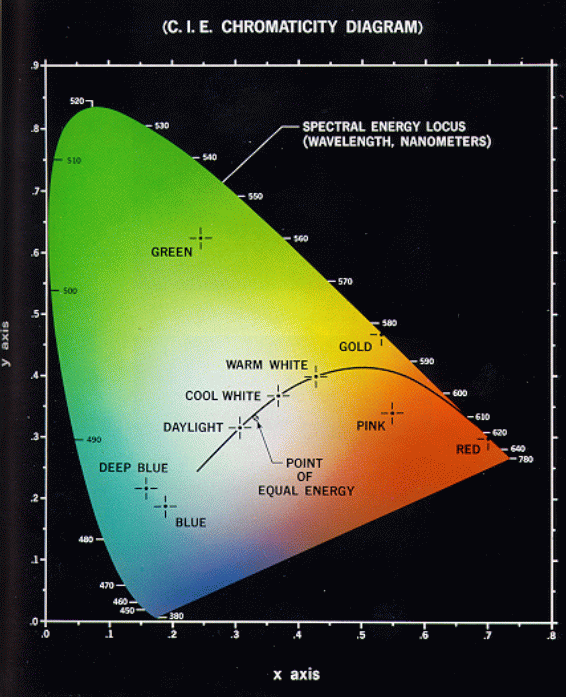
All visible colors are represented by the points inside an enclosed area in the $X+Y+Z=1$ plane. And the chromaticity diagram is the projection of this enclosed area on $(X,Y)$ plane.