


Next: Three Components of Color
Up: The Color Space
Previous: RGB Primaries of Color
As we have seen, any three linearly independent colors can be considered as
the primary colors and used as the bases of the 3D color space. Therefore the
same color may be represented by different tristimulus values under different
color systems of different primaries. For example, consider color 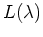 matched in the color space by two sets of primaries
matched in the color space by two sets of primaries
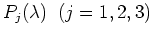 and
and
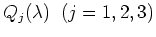 :
:
As all terms in this equation are matching colors, they must all cause the same
receptor responses:
To find the relationship between the two sets of tristimulus values
![$[A_1, A_2, A_3]$](img156.png) and
and
![$[B_1, B_2, B_3]$](img157.png) , we first consider matching the second
set of primaries by the first set:
, we first consider matching the second
set of primaries by the first set:
Note that in general 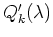 and
and 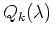 do not have identical
spectral energy distributions, but they are matching colors represented by the
same point in the 3D color space. Now we can use
do not have identical
spectral energy distributions, but they are matching colors represented by the
same point in the 3D color space. Now we can use 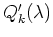 's as the
primaries to match the color
's as the
primaries to match the color 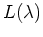 so that
so that
The last equation is due to the fact that this color is also matched by
the primary 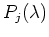 's as assumed originally, and can be written as
's as assumed originally, and can be written as
As in general
we must have
Now the relationship between the two sets of primaries can be summarized as
- For the primaries:
- For the tristimulus values:
To express the above relationship in matrix form, define
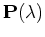 ,
,
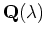 ,
, 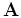 and
and 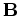 :
as 3D vectors
:
as 3D vectors
and 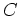 as a 3 by 3 matrix
as a 3 by 3 matrix
and we have
and
where
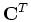 represents the transpose of matrix
represents the transpose of matrix
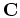 .
These linear relations are called projective transforms.
.
These linear relations are called projective transforms.



Next: Three Components of Color
Up: The Color Space
Previous: RGB Primaries of Color
Ruye Wang
2013-09-25
![]() matched in the color space by two sets of primaries
matched in the color space by two sets of primaries
![]() and
and
![]() :
:
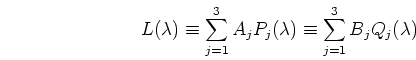
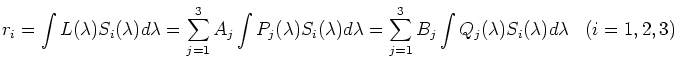
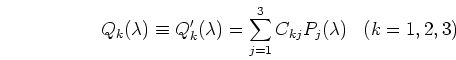
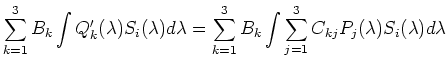
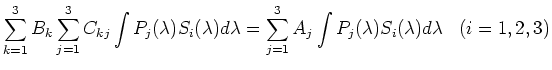
![\begin{displaymath}\sum_{j=1}^3 [ A_j-\sum_{k=1}^3 C_{kj} B_k ]
\int P_j(\lambda) S_i(\lambda) d\lambda =0 \;\;\;(i=1,2,3) \end{displaymath}](img165.png)
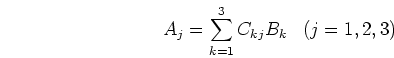
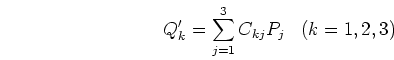
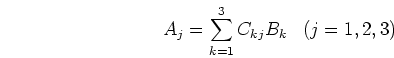
![\begin{displaymath}\mbox{{\bf C}}\stackrel{\triangle}{=}\left[ \begin{array}{lll...
...22} & C_{23} \\
C_{31} & C_{32} & C_{33} \end{array} \right] \end{displaymath}](img178.png)