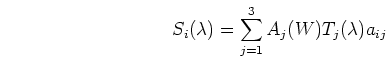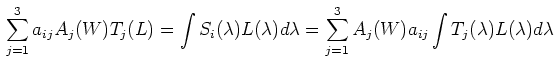Next: CIE's Spectral RGB Primaries
Up: Trichromatic Theory Revisited
Previous: Calibration with a Reference
If the color to be matched is a spectral color of a single wavelength
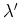 with unit energy:
with unit energy:
the matching equations become
Solving these three simultaneous equations we can get the tristimulus values
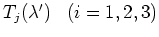 for the given spectral color
for the given spectral color
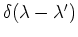 . As functions of wavelength
. As functions of wavelength 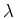 , these
, these
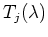 's are called the spectral matching curves representing
amount of each primary needed to match a flat spectral distribution.
's are called the spectral matching curves representing
amount of each primary needed to match a flat spectral distribution.
The spectral matching curves can also be used to obtain tristimulus values
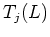 for any given color
for any given color 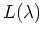 . To see this, we substitute
. To see this, we substitute
into the color matching equations to get
As this equation holds for all three types of cells (i=1,2,3), we see that
the tristimulus values for matching any color 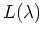 can be easily
obtained from the spectral matching curves
can be easily
obtained from the spectral matching curves 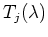 .
.
Ruye Wang
2013-09-25
![]() with unit energy:
with unit energy:
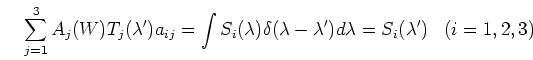
![]() for any given color
for any given color ![]() . To see this, we substitute
. To see this, we substitute