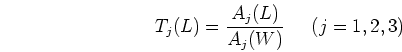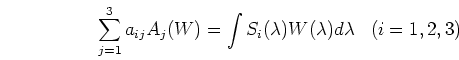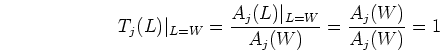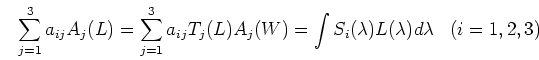Next: Spectral matching curves
Up: Trichromatic Theory Revisited
Previous: Theory of Color Matching
The absolute magnitudes of the weights 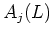 is directly affected by the
intensity of the given color
is directly affected by the
intensity of the given color 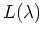 . To calibrate various intensities,
we normalize
. To calibrate various intensities,
we normalize 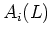 's by comparing them against a reference white light
source
's by comparing them against a reference white light
source 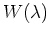 .
.
As discussed before, we define the tristimulus values of a given color
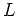 as
as
where 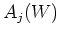 's are the weights for the three primaries to match the
reference white
's are the weights for the three primaries to match the
reference white 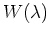 .
. 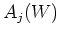 's can be obtained by solving the
matching equations for the reference white:
's can be obtained by solving the
matching equations for the reference white:
In particular, the tristimulus values for the reference white itself is
always 1:
Now the color matching equations for an arbitrary color 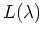 become
become
Solving these equations, we can get
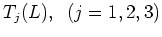 for matching any
given color
for matching any
given color 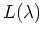 .
.
Ruye Wang
2013-09-25
![]() is directly affected by the
intensity of the given color
is directly affected by the
intensity of the given color ![]() . To calibrate various intensities,
we normalize
. To calibrate various intensities,
we normalize ![]() 's by comparing them against a reference white light
source
's by comparing them against a reference white light
source ![]() .
.
![]() as
as