


Next: Calibration with a Reference
Up: Trichromatic Theory Revisited
Previous: Trichromatic Theory Revisited
Now we can revisit the color matching issue, and discuss the real meaning
of the equivalent symbol 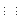 .
.
The visual system and the color system are described by
- The Visual System: The three types of photoreceptors with
sensitivities
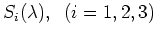 ;
;
- The Color System: The three primaries with energy spectral
distributions
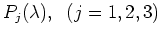 together with the
reference white
together with the
reference white 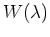 .
.
We want to match a given color 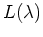 with another color produced by
mixing the three primaries
with another color produced by
mixing the three primaries
with proper weights or intensities
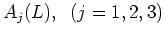 .
.
Since color matching now means specifically that the three types of
photoreceptors have the same responses to the two colors, we must require
where 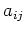 is defined as the response of the ith photoreceptors to the jth
primary:
is defined as the response of the ith photoreceptors to the jth
primary:
The three equations above can now be rewritten to obtain the color
matching equations:
Solving this set of three simultaneous equations, we get the three coefficients
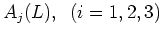 , the weights for mixing the three primaries to produce
color
, the weights for mixing the three primaries to produce
color
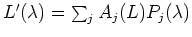 , which will be perceived the
same as the given color
, which will be perceived the
same as the given color 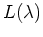 :
:
However, we note that these two functions do not equate mathematically in
general, i.e., they are different energy spectral distributions:
In general if the three types of photoreceptors' responses to two colors
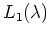 and
and 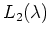 are the same, i.e.,
are the same, i.e.,
then the two colors are indistinguishable and are called metamers.
There are infinitely many possible metameric spectral energy distributions
that cause the same responses in the visual system.



Next: Calibration with a Reference
Up: Trichromatic Theory Revisited
Previous: Trichromatic Theory Revisited
Ruye Wang
2013-09-25
![]() .
.
![]() with another color produced by
mixing the three primaries
with another color produced by
mixing the three primaries
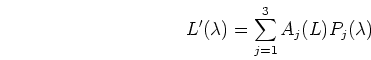
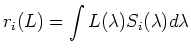
![$\displaystyle r_i(L')= \int L'(\lambda) S_i(\lambda) d\lambda
= \int [ \sum_{j=1}^3 A_j(L) P_j(\lambda) ]
S_i(\lambda) d\lambda$](img82.png)
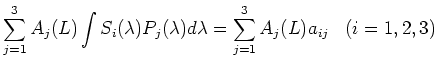
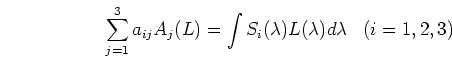
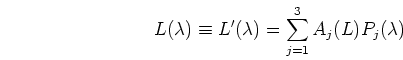
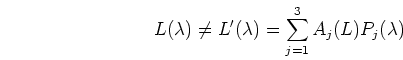
![]() and
and ![]() are the same, i.e.,
are the same, i.e.,