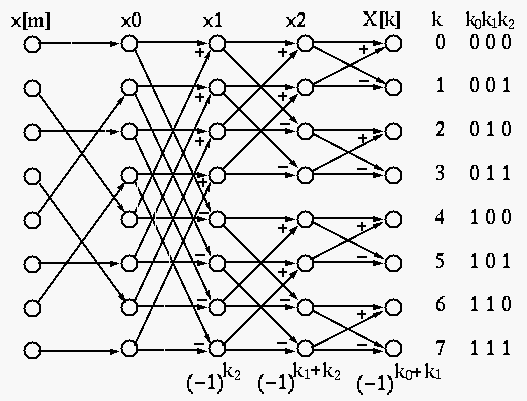The sequency-ordered Walsh-Hadamard transform (![]() , also called Walsh
ordered
, also called Walsh
ordered ![]() ) can be obtained by first carrying out the fast
) can be obtained by first carrying out the fast ![]() and then
reordering the components of
and then
reordering the components of ![]() as shown above. Alternatively, we can
use the following fast
as shown above. Alternatively, we can
use the following fast ![]() directly with better efficiency.
directly with better efficiency.
The sequency ordered WHT of ![]() can also be defined as
can also be defined as
![\begin{displaymath}X[k]=\sum_{m=0}^{N-1} w[k,m] x[m]
=\sum_{m=0}^{N-1} x[m] \prod_{i=0}^{n-1} (-1)^{(k_i+k_{i+1})m_{n-1-i}}
\end{displaymath}](img82.png)
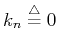 , and the exponent of
, and the exponent of
In the following, we assume
![]() , and we represent
, and we represent ![]() and
and ![]() in binary form as, respectively,
in binary form as, respectively,
![]() and
and ![]() , i.e.,
, i.e.,
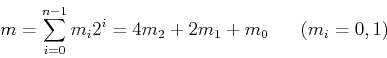
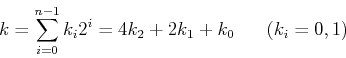
As the first step of the algorithm, we rearrange the order of the samples
![]() by bit-reversal to get
by bit-reversal to get
![$\displaystyle \sum_{m_2=0}^1 \sum_{m_1=0}^1 \sum_{m_0=0}^1 x_0[4m_0+2m_1+m_2]
\prod_{i=0}^2 (-1)^{(k_i+k_{i+1}) m_{n-1-i}}$](img93.png) |
|||
![$\displaystyle \sum_{l_0=0}^1 \sum_{l_1=0}^1 \sum_{l_2=0}^1 x_0[4l_2+2l_1+l_0]
\prod_{i=0}^2 (-1)^{(k_i+k_{i+1})l_i}$](img94.png) |
![$\displaystyle \sum_{l_0=0}^1 \sum_{l_1=0}^1
\prod_{i=0}^1 (-1)^{(k_i+k_{i+1})l_i}
[ x_0[2l_1+l_0)+(-1)^{k_2+k_3} x_0[4+2l_1+l_0] ]$](img95.png) |
|||
![$\displaystyle \sum_{l_0=0}^1 \sum_{l_1=0}^1 \prod_{i=0}^1
(-1)^{(k_i+k_{i+1})l_i} x_1[4k_2+2l_1+l_0]$](img96.png) |
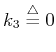 and
and | (11) |
![$\displaystyle \sum_{l_0=0}^1 (-1)^{(k_i+k_{i+1})l_0}
[ x_1[4k_2+l_0]+(-1)^{k_1+k_2} x_1[4k_2+2+l_0] ]$](img100.png) |
|||
![$\displaystyle \sum_{l_0=0}^1 (-1)^{(k_i+k_{i+1})l_0}
x_2[4k_2+2k_1+m_0]$](img101.png) |
| (12) |
| (13) |
Summarizing the above steps, we get the fast ![]() algorithm composed of
the bit-reversal and the three equations (11), (12), and (13), as illustrated
below:
algorithm composed of
the bit-reversal and the three equations (11), (12), and (13), as illustrated
below: