


Next: About this document ...
Up: wht
Previous: Fast Walsh-Hadamard Transform (Sequency
Consider a signal vector of N=4 elements (samples):
The corresponding 4 by 4 WHT matrix (Hadamard ordered) is:
The rows (or colums) of this matrix can be reordered according to their sequency
by the following mapping:
to get the sequency ordered (also called Walsh ordered) matrix
where 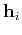 is the ith colum (or row) vector of the symmetric matrix
is the ith colum (or row) vector of the symmetric matrix
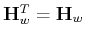 representing a square wave of sequency
representing a square wave of sequency 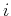 (with
(with 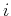 zero-crossings). Now the sequency spectrum of the signal can be found as
zero-crossings). Now the sequency spectrum of the signal can be found as
and the inverse transform (note 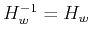 ) represents the signal vector as
a linear combination of a set of square waves of different sequencies:
) represents the signal vector as
a linear combination of a set of square waves of different sequencies:
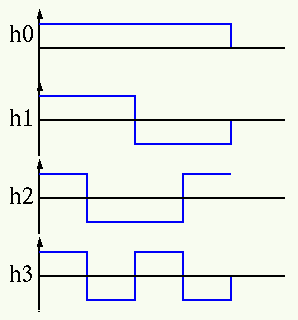
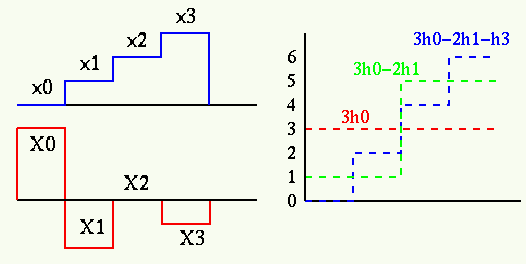
We can also verify that indeed the inverse transform will produce the original
signal from its spectrum:



Next: About this document ...
Up: wht
Previous: Fast Walsh-Hadamard Transform (Sequency
Ruye Wang
2013-10-22
![\begin{displaymath}{\bf H}_h=\frac{1}{2} \left[ \begin{array}{rrrr} 1 & 1 & 1 & ...
...& -1 1 & 1 & -1 & -1 1 & -1 & -1 & 1 \end{array} \right]
\end{displaymath}](img106.png)

![\begin{displaymath}{\bf H}_w=\frac{1}{2} \left[ \begin{array}{rrrr} 1 & 1 & 1 & ...
...1 & 1 & -1 \end{array} \right]=\frac{1}{2}[h_0, h_1, h_2, h_3]
\end{displaymath}](img108.png)
![\begin{displaymath}{\bf X}={\bf H}_w {\bf x} =\frac{1}{2} \left[ \begin{array}{r...
...\left[ \begin{array}{r} 3 -2 0 -1 \end{array} \right] \end{displaymath}](img112.png)
![\begin{displaymath}
{\bf x}={\bf H}_w {\bf X}=\frac{1}{2}[h_0, h_1, h_2, h_3]
...
... -2 0 -1 \end{array} \right]
=\frac{3h_0-2h_1-h_3}{2}
\end{displaymath}](img114.png)


![\begin{displaymath}{\bf x}={\bf H}_w {\bf X}=\frac{1}{2}\left[ \begin{array}{rrr...
... =\left[ \begin{array}{c} 0 1 2 3 \end{array} \right]
\end{displaymath}](img115.png)