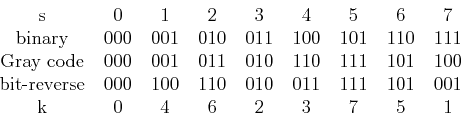Next: Fast Walsh-Hadamard Transform (Sequency
Up: wht
Previous: The Walsh-Hadamard Transform (Hadamard
In order for the elements in the spectrum
![${\bf X}=[ X[0], X[1], \cdots, X[N-1] ]^T$](img40.png) to represent different sequency components contained in the
signal in a low-to-high order, we can re-order the rows (or columns) of
the Hadamard matrix
to represent different sequency components contained in the
signal in a low-to-high order, we can re-order the rows (or columns) of
the Hadamard matrix 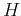 according to their sequencies.
according to their sequencies.
The conversion of a given sequency 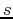 into the corresponding index number
into the corresponding index number
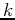 in Hadamard order is a three-step process:
in Hadamard order is a three-step process:
- represent
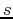 in binary form:
in binary form:
- convert this binary form to Gray code:
where 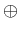 represents exclusive or and
represents exclusive or and 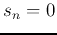 by definition.
by definition.
- bit-reverse
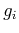 's to get
's to get 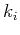 's:
's:
Now 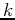 can be found as
can be found as
where 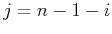 or equivalently
or equivalently 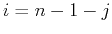 .
.
For example,
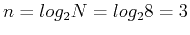 , we have
, we have
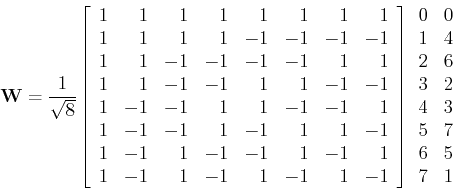
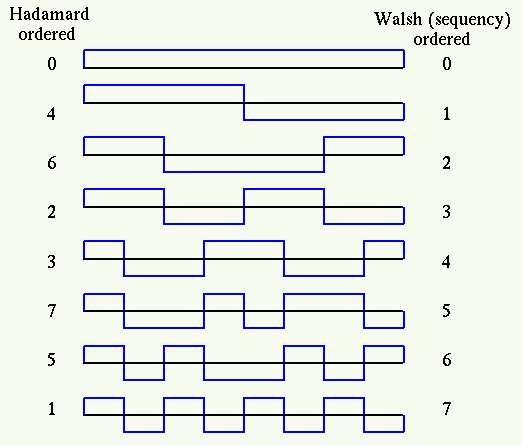
Now the sequency-ordered or Walsh-ordered Walsh-Hadamard matrix can be
obtained as
The first column on the right of the matrix is for the sequency 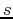 of
the corresponding row, which is the index for the sequency-ordered
matrix, and the second column is the index
of
the corresponding row, which is the index for the sequency-ordered
matrix, and the second column is the index 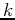 of the Hadamard ordered.
We see that this matrix is still symmetric:
of the Hadamard ordered.
We see that this matrix is still symmetric:



Next: Fast Walsh-Hadamard Transform (Sequency
Up: wht
Previous: The Walsh-Hadamard Transform (Hadamard
Ruye Wang
2013-10-22
![]() to represent different sequency components contained in the
signal in a low-to-high order, we can re-order the rows (or columns) of
the Hadamard matrix
to represent different sequency components contained in the
signal in a low-to-high order, we can re-order the rows (or columns) of
the Hadamard matrix ![]() according to their sequencies.
according to their sequencies.
![]() into the corresponding index number
into the corresponding index number
![]() in Hadamard order is a three-step process:
in Hadamard order is a three-step process:
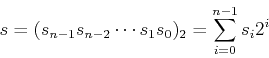
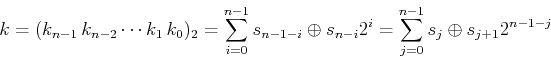
![]() , we have
, we have