


Next: Sequency Ordered Walsh-Hadamard Matrix
Up: wht
Previous: Hadamard Matrix
As any orthogonal (unitary) matrix can be used to define a discrete
orthogonal (unitary) transform, we define a Walsh-Hadamard transform of
Hadamard order (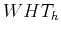 ) as
) as
These are the forward and inverse 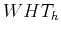 transform pair. Note that the
forward and inverse transforms are identical!
transform pair. Note that the
forward and inverse transforms are identical!
Here
![${\bf x}=[ x[0], x[1], \cdots, x[N-1] ]^T$](img39.png) and
and
![${\bf X}=[ X[0], X[1], \cdots, X[N-1] ]^T$](img40.png) are the signal
and spectrum vectors, respectively. The
are the signal
and spectrum vectors, respectively. The 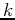 th element of the transform
can also be written as
th element of the transform
can also be written as
The complexity of WHT is 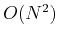 . Similar to FFT algorithm, we can derive a
fast WHT algorithm with complexity of
. Similar to FFT algorithm, we can derive a
fast WHT algorithm with complexity of 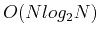 . We will assume
. We will assume  and
and
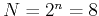 in the following derivation. An
in the following derivation. An 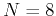 point
point 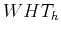 of signal
of signal ![$x[m]$](img45.png) is defined as
is defined as
Here for simplicity, we ignored the coefficient 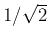 .
This equation can be separated into two parts. The first half of the
.
This equation can be separated into two parts. The first half of the 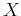 vector can be obtained as
vector can be obtained as
![\begin{displaymath}
\left[ \begin{array}{c} X[0] X[1] X[2] X[3] \end{ar...
...ay}{c} x_1[0] x_1[1] x_1[2] x_1[3] \end{array}\right]
\end{displaymath}](img49.png) |
(1) |
where
![\begin{displaymath}
x_1[i] \stackrel{\triangle}{=}x[i]+x[i+4] \;\;\;\;(i=0, \cdots ,3)
\end{displaymath}](img50.png) |
(2) |
The second half of the 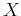 vector can be obtained as
vector can be obtained as
![\begin{displaymath}
\left[ \begin{array}{c} X[4] X[5] X[6] X[7] \end{ar...
...ay}{c} x_1[4] x_1[5] x_1[6] x_1[7] \end{array}\right]
\end{displaymath}](img51.png) |
(3) |
where
![\begin{displaymath}
x_1[i+4] \stackrel{\triangle}{=}x[i]-x[i+4] \;\;\;\;(i=0, \cdots ,3)
\end{displaymath}](img52.png) |
(4) |
What we have done is converting a  of size
of size 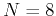 into two
into two 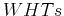 of
size
of
size 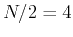 . Continuing this process recursively, we can rewrite Eq. (1)
as the following (similar process for Eq. (3))
. Continuing this process recursively, we can rewrite Eq. (1)
as the following (similar process for Eq. (3))
This equation can again be separated into two halves. The first half is
![\begin{displaymath}
\left[ \begin{array}{c} X[0] X[1] \end{array} \right]
={\...
...{array}{c} x_2[0]+x_2[1] x_2[0]-x_2[1] \end{array} \right]
\end{displaymath}](img57.png) |
(5) |
where
![\begin{displaymath}
x_2[i] \stackrel{\triangle}{=}x_1[i]+x_1[i+2]\;\;\;\;(i=0,1)
\end{displaymath}](img58.png) |
(6) |
The second half is
![\begin{displaymath}
\left[ \begin{array}{c} X[2] X[3] \end{array} \right]
={\...
...{array}{c} x_2[2]+x_2[3] x_2[2]-x_2[3] \end{array} \right]
\end{displaymath}](img59.png) |
(7) |
where
![\begin{displaymath}
x_2[i+2] \stackrel{\triangle}{=}x_1[i]-x_1[i+2]\;\;\;\;(i=0,1)
\end{displaymath}](img60.png) |
(8) |
![$X[4]$](img61.png) through
through ![$X[7]$](img62.png) of the second half can be obtained similarly.
of the second half can be obtained similarly.
![\begin{displaymath}
X[0]=x_2[0]+x_2[1]
\end{displaymath}](img63.png) |
(9) |
and
![\begin{displaymath}
X[1]=x_2[0]-x_2[1]
\end{displaymath}](img64.png) |
(10) |
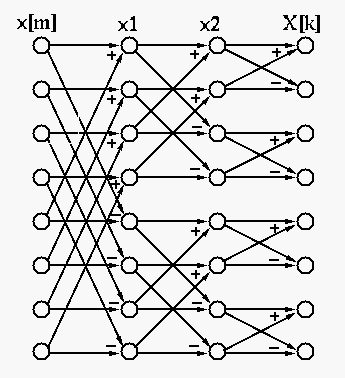
Summarizing the above steps of Equations (2), (4), (6), (8), (9) and (10),
we get the Fast WHT algorithm as illustrated below.



Next: Sequency Ordered Walsh-Hadamard Matrix
Up: wht
Previous: Hadamard Matrix
Ruye Wang
2013-10-22
![]() ) as
) as
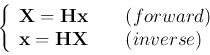
![]() and
and
![]() are the signal
and spectrum vectors, respectively. The
are the signal
and spectrum vectors, respectively. The ![]() th element of the transform
can also be written as
th element of the transform
can also be written as
![\begin{displaymath}X[k]=\sum_{m=0}^{N-1}h[k,m] x[m]
=\sum_{m=0}^{N-1}x[m] \prod_{i=0}^{n-1}(-1)^{m_ik_i} \end{displaymath}](img41.png)
![\begin{displaymath}
{\bf X}=
\left[ \begin{array}{c} X[0] \vdots X[3] X...
... \vdots x[3] x[4] \vdots x[7]
\end{array} \right]
\end{displaymath}](img46.png)
![\begin{displaymath}
\left[ \begin{array}{c} X[0] X[1] X[2] X[3] \end{ar...
...ay}{c} x_1[0] x_1[1] x_1[2] x_1[3] \end{array}\right]
\end{displaymath}](img49.png)
![\begin{displaymath}
\left[ \begin{array}{c} X[4] X[5] X[6] X[7] \end{ar...
...ay}{c} x_1[4] x_1[5] x_1[6] x_1[7] \end{array}\right]
\end{displaymath}](img51.png)
![]() of size
of size ![]() into two
into two ![]() of
size
of
size ![]() . Continuing this process recursively, we can rewrite Eq. (1)
as the following (similar process for Eq. (3))
. Continuing this process recursively, we can rewrite Eq. (1)
as the following (similar process for Eq. (3))
![\begin{displaymath}
\left[ \begin{array}{c} X[0] X[1] X[2] X[3] \end{ar...
...{c} x_1[0] x_1[1] x_1[2] x_1[3] \end{array}
\right]
\end{displaymath}](img56.png)
![\begin{displaymath}
\left[ \begin{array}{c} X[0] X[1] \end{array} \right]
={\...
...{array}{c} x_2[0]+x_2[1] x_2[0]-x_2[1] \end{array} \right]
\end{displaymath}](img57.png)
![\begin{displaymath}
\left[ \begin{array}{c} X[2] X[3] \end{array} \right]
={\...
...{array}{c} x_2[2]+x_2[3] x_2[2]-x_2[3] \end{array} \right]
\end{displaymath}](img59.png)
