The Kronecker product of two matrices
![]() and
and
![]() is defined as
is defined as
![\begin{displaymath}{\bf A} \otimes {\bf B} \stackrel{\triangle}{=}\left[ \begin{...
...B} & \cdots & a_{mn}{\bf B} \end{array} \right]_{mk \times nl} \end{displaymath}](img3.png)
In general,
![]() .
.
The Hadamard Matrix is defined recursively as below:
![\begin{displaymath}{\bf H}_1 \stackrel{\triangle}{=} \frac{1}{\sqrt{2}} \left[
\begin{array}{rr} 1 & 1 1 & -1 \end{array} \right] \end{displaymath}](img5.png)
![\begin{displaymath}
{\bf H}_n={\bf H}_1\otimes{\bf H}_{n-1}=\frac{1}{\sqrt{2}}\...
...}_{n-1} {\bf H}_{n-1} & -{\bf H}_{n-1} \end{array} \right]
\end{displaymath}](img6.png)
![\begin{displaymath}{\bf H}_2={\bf H}_1 \otimes {\bf H}_1=\frac{1}{\sqrt{2}}\left...
...
1 & 1 & -1 & -1 1 & -1 & -1 & 1 \\
\end{array} \right]
\end{displaymath}](img10.png)
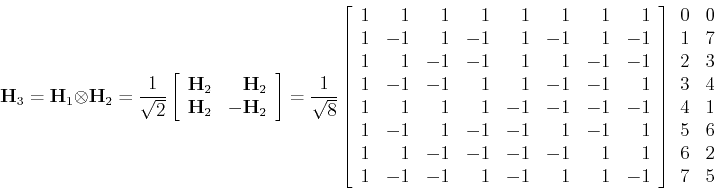
The first column on the right of the matrix ![]() is for the
indecies of the
is for the
indecies of the ![]() rows, and the second column represents the
sequency (the number of zero-crossings or sign changes) in
each row. Sequency is similar to but different from frequency in the
sense that it measures the rate of change of non-periodical signals.
rows, and the second column represents the
sequency (the number of zero-crossings or sign changes) in
each row. Sequency is similar to but different from frequency in the
sense that it measures the rate of change of non-periodical signals.
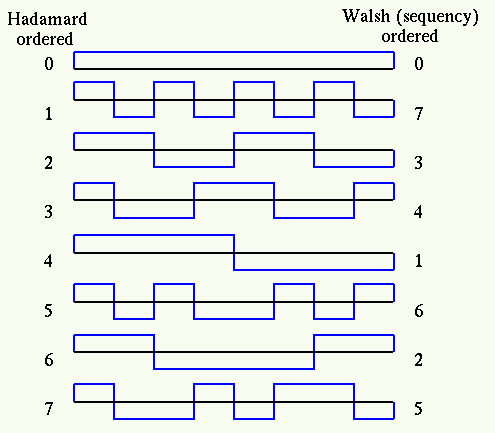
The rows of the matrix can be considered as the ![]() samples of the following waveforms:
samples of the following waveforms:
The Hadamard matrix can also be obtained by defining its element in
the kth row and mth column of ![]() as
as
![\begin{displaymath}h[k,m]=(-1)^{\sum_{i=0}^{n-1}k_im_i}
=\prod_{i=0}^{n-1} (-1)^{k_im_i}=h[m,k] \;\;\;\;\;
(k,m=0,1,\cdots,N-1)\end{displaymath}](img18.png)
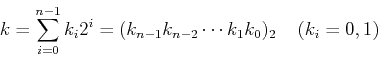
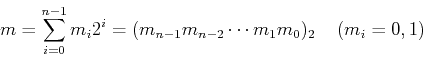
We can show the Hadamard matrix ![]() is orthogonal by induction.
First, it is obvious that
is orthogonal by induction.
First, it is obvious that ![]() is orthogonal:
is orthogonal:
![\begin{displaymath}
{\bf H}_1^T{\bf H}_1={\bf H}_1{\bf H}_1
=\frac{1}{2}\left[...
...egin{array}{rr}1&0 0&1\end{array}\right]={\bf I}_{2\times 2}
\end{displaymath}](img28.png)
![$\displaystyle \frac{1}{2}\left[ \begin{array}{rr}
{\bf H}_{n-1} & {\bf H}_{n-...
...f H}_{n-1} & {\bf H}_{n-1} {\bf H}_{n-1}&-{\bf H}_{n-1} \end{array} \right]$](img34.png) |
|||
![$\displaystyle \frac{1}{2}\left[\begin{array}{rr}{\bf H}_{n-1}{\bf H}_{n-1}+{\bf...
...\bf H}_{n-1}+{\bf H}_{n-1}{\bf H}_{n-1}\end{array}\right]
={\bf I}_{N\times N}$](img35.png) |
In summary, the Hadamard matrix ![]() is real, symmetric, and orthogonal:
is real, symmetric, and orthogonal: