


Next: Fast Wavelet Transform (FWT)
Up: wavelets
Previous: Wavelet Expansion
The discrete signal
![${\bf x}=[x[0],\cdots,x[N-1]]^T$](img146.png) is a set of N samples taken
from a continuous signal
is a set of N samples taken
from a continuous signal
for some initial time 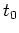 and sampling period
and sampling period 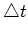 . The basis functions
. The basis functions
![${\bf\varphi}=[\varphi[0],\cdots,\varphi[N-1]]^T$](img150.png) and
and
![${\bf\psi}=[\psi[0],\cdots,
\psi[N-1]]^T$](img151.png) are also vectors containing
are also vectors containing 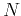 elements. We let
elements. We let 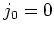 ,
, 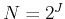 ,
,
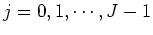 and
and
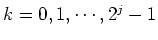 . Correspondingly the wavelet expansion
becomes discrete wavelet transform (DWT). The discrete function is represented as
a weighted sum in the space spanned by the bases
. Correspondingly the wavelet expansion
becomes discrete wavelet transform (DWT). The discrete function is represented as
a weighted sum in the space spanned by the bases 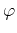 and
and 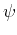 :
:
This is the inverse wavelet transform where the summation over 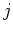 is for different
scale levels and the summation over
is for different
scale levels and the summation over 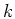 is for different translations in each scale
level, and the coefficients (weights) are projections of the function onto each of
the basis functions:
is for different translations in each scale
level, and the coefficients (weights) are projections of the function onto each of
the basis functions:
where
![$W_{\varphi}[j_0,k]$](img161.png) is called the approximation coefficient and
is called the approximation coefficient and
![$W_{\psi}[j,k]$](img162.png) is called the detail coefficient. These are the forward
wavelet transform.
is called the detail coefficient. These are the forward
wavelet transform.
An Example:
Assume 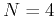 -point discrete singal
-point discrete singal
![${\bf x}=[x[0],\cdots,x[N-1]]^T=[1, 4, -3, 0]^T$](img164.png) and the discrete Haar scaling and wavelet functions are:
and the discrete Haar scaling and wavelet functions are:
The coefficient for 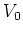 :
:
The coefficient for 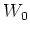 :
:
The two coefficients for 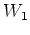 :
:
In matrix form, we have
Now the function ![$x[m]$](img171.png) can be expressed as a linear combination of these basis
functions:
can be expressed as a linear combination of these basis
functions:
or in matrix form:



Next: Fast Wavelet Transform (FWT)
Up: wavelets
Previous: Wavelet Expansion
Ruye Wang
2008-12-16
![]() is a set of N samples taken
from a continuous signal
is a set of N samples taken
from a continuous signal
![\begin{displaymath}
x[m]=\frac{1}{\sqrt{N}}\sum_k W_{\varphi}[j_0,k]\varphi_{j_0...
... \sum_k W_{\psi}[j,k]\psi_{j,k}[m],
\;\;\;\;\;(m=0,\cdots,N-1) \end{displaymath}](img158.png)
![\begin{displaymath}W_{\varphi}[j_0,k]=({\bf x},{\bf\varphi}_{j_0,k})=\frac{1}{\s...
...=0}^{N-1} x[m] \varphi_{j_0,k}[m],\;\;\;\;\mbox{(for all $k$)} \end{displaymath}](img159.png)
![\begin{displaymath}W_{\psi}[j,k]=({\bf x},{\bf\psi}_{j,k})=\frac{1}{\sqrt{N}}\su...
...m] \psi_{j,k}[m],\;\;\;\;\mbox{(for all $k$ and all $j>j_0$)} \end{displaymath}](img160.png)
![]() -point discrete singal
-point discrete singal
![]() and the discrete Haar scaling and wavelet functions are:
and the discrete Haar scaling and wavelet functions are:
![\begin{displaymath}\left[ \begin{array}{rrrr}
1 & 1 & 1 & 1 1 & 1 & -1 & -1 \...
... \psi_{0,0}[m] \psi_{1,0}[m] \psi_{1,1}[m]
\end{array}\end{displaymath}](img165.png)
![\begin{displaymath}W_{\varphi}[0,0]=\frac{1}{2}\sum_{m=0}^3 x[m]\varphi_{0,0}[m]
=\frac{1}{2}[1\cdot 1+4\cdot 1-3\cdot 1+0\cdot 1]=1 \end{displaymath}](img166.png)
![\begin{displaymath}W_{\psi}[0,0]=\frac{1}{2}\sum_{m=0}^3 x[m]\psi_{0,0}[m]
=\frac{1}{2}[1\cdot 1+4\cdot 1-3\cdot (-1)+0\cdot (-1)]=4 \end{displaymath}](img167.png)
![\begin{displaymath}W_{\psi}[1,0]=\frac{1}{2}\sum_{m=0}^3 x[m]\psi_{1,0}[m]
=\fr...
...ot \sqrt{2}+4\cdot (-\sqrt{2})-3\cdot 0+0\cdot 0]=-1.5\sqrt{2} \end{displaymath}](img168.png)
![\begin{displaymath}W_{\psi}[1,1]=\frac{1}{2}\sum_{m=0}^3 x[m]\psi_{1,0}[m]
=\fr...
...ot 0+4\cdot 0-3\cdot \sqrt{2}+0\cdot (-\sqrt{2})]=-1.5\sqrt{2} \end{displaymath}](img169.png)
![\begin{displaymath}\left[ \begin{array}{c} 1 4 -1.5\sqrt{2} -1.5\sqrt{2} ...
...t]
\left[ \begin{array}{c} 1 4 -3 0 \end{array} \right]
\end{displaymath}](img170.png)
![\begin{displaymath}\left[ \begin{array}{r} 1 4 -3 0 \end{array} \right]
=...
...y}{c} 1 4 -1.5\sqrt{2} -1.5\sqrt{2} \end{array} \right]
\end{displaymath}](img173.png)