


Next: 2D DWT
Up: wavelets
Previous: Discrete Wavelet Transform
As shown before, the discrete wavelet transform of a discrete signal
![${\bf x}=[x[0],\cdots,x[N-1]]^T$](img146.png) is the process of getting the coefficients:
is the process of getting the coefficients:
where the basis scaling and wavelet functions are respectively
Recall that both the scaling and wavelet functions can be expanded in terms
of the basis scaling functions of the next higher resolution:
We now consider a fast algorithm to obtain the coefficients
![$W_{\varphi}[j,k]$](img178.png) and
and
![$W_{\psi}[j,k]$](img162.png) of different scales
of different scales 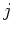 . Consider first the scaling function
. Consider first the scaling function
![$\varphi[m]$](img179.png) . Replacing
. Replacing 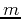 by
by 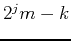 (scaled by
(scaled by 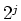 and translated by
and translated by 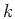 ),
we get
),
we get
We then let 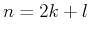 i.e.
i.e. 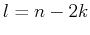 , the above becomes
, the above becomes
Similarly, the wavelet function can also be expanded:
This wavelet function is identical to the one used in the discrete wavelet transform
above, which can be replaced by the right-hand side of the equation:
Note that the expression inside the brackets happens to be the wavelet transform
for the coefficient of scale 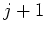 :
:
therefore we have a recursive relation between the wavelet transform coefficients
of two consecutive scale levels 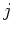 and
and 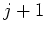 :
:
and the same is true to the scaling function:
Comparing these equations with a discrete convolution:
we see that the wavelet transform coefficients
![$W_{\varphi}[j,k]$](img178.png) and
and ![$W_{\psi}[j,k]$](img162.png) at the jth scale can be obtained from the coefficients
at the jth scale can be obtained from the coefficients
![$W_{\varphi}[j+1,k]$](img196.png) and
and
![$W_{\psi}[j+1,k]$](img197.png) at the (j+1)th scale by:
at the (j+1)th scale by:
- Convolution with time-reversed
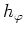 or
or 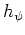 ;
;
- Sub-sampling to get every other samples in the convolution.
We can therefore write
Based on these two equations, all wavelet and scaling coefficients ![$W_{\psi}[j,k]$](img162.png) and
and
![$W_{\varphi}[j,k]$](img178.png) of a given signal
of a given signal 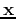 can be obtained recursively
from the coefficients
can be obtained recursively
from the coefficients ![$W_{\psi}[J,k]$](img200.png) and
and
![$W_{\varphi}[j,k]$](img178.png) at the highest
resolution level
at the highest
resolution level 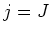 (with maximum details), i.e., the
(with maximum details), i.e., the 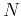 data points
data points ![$x[m]$](img171.png) (
(
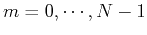 ) directly sampled from the signal
) directly sampled from the signal 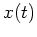 . As a member of space
. As a member of space
 , these discrete samples can be written as a linear combination of the scaling
basis functions
, these discrete samples can be written as a linear combination of the scaling
basis functions
![$\varphi_{J,k}[m]$](img204.png) :
:
If we let the kth basis function be a unit pulse at the kth sampling time, i.e.,
![$\varphi_{J,k}[m]=\delta[k-m]$](img206.png) (same as the ith component of a unit vector
(same as the ith component of a unit vector
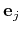 in N-dimensional vector space is
in N-dimensional vector space is
![$e_{ij}=\delta[i-j]$](img208.png) ), then the kth
coefficient
), then the kth
coefficient
![$W_{\varphi}[J,k]$](img209.png) is the same as the kth sample of the function
is the same as the kth sample of the function 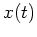 .
I.e.,
.
I.e.,
![$W_{\varphi}[J,k]=x(k)$](img210.png) , from which the scaling and wavelet coefficients of
the lower scales
, from which the scaling and wavelet coefficients of
the lower scales 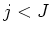 can be obtained by the subsequent filter banks.
can be obtained by the subsequent filter banks.
Inverse Wavelet Transform
As the forward wavelet transform - finding the transform coefficients 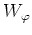 and
and 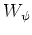 from a given function
from a given function 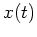 - can be implemented by
the analysis filter bank, the inverse wavelet transform - reconstructing the function
- can be implemented by
the analysis filter bank, the inverse wavelet transform - reconstructing the function
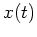 from the coefficients
from the coefficients 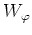 and
and 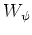 - can be implemented by
the synthesis filter bank.
- can be implemented by
the synthesis filter bank.
Complexity of FWT
The computation cost of the fast wavelet transform (FWT) is the convolutions carried
out in each of the filters. The number of data samples in the convolution is halved
after each sub-sampling, therefore the total complexity is:
i.e., the FWT has linear complexity.
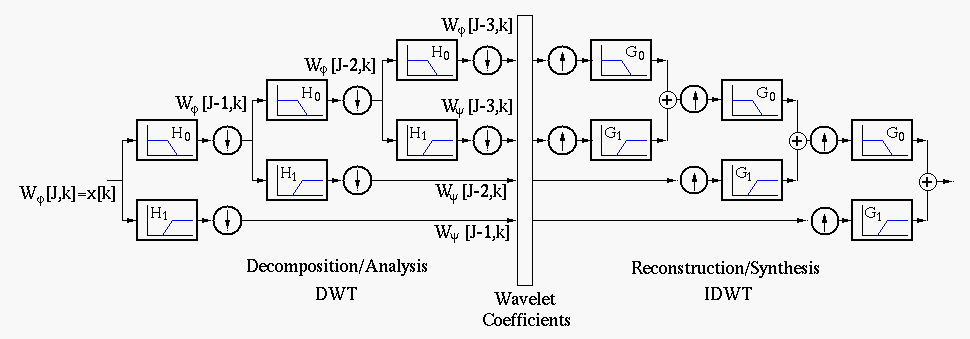
The system shown in the figure above is called a filter bank and is further discussed
here
A detailed discussion about Matlab implementaton can be found on this
MathWorks webpage.



Next: 2D DWT
Up: wavelets
Previous: Discrete Wavelet Transform
Ruye Wang
2008-12-16
![]() is the process of getting the coefficients:
is the process of getting the coefficients:
![\begin{displaymath}W_{\varphi}[j_0,k]=\frac{1}{\sqrt{N}}\sum_{m=0}^{N-1} x[m] \v...
...m] 2^{j_0/2}\varphi[2^{j_0} m-k],
\;\;\;\;\mbox{(for all $k$)} \end{displaymath}](img174.png)
![\begin{displaymath}W_{\psi}[j,k]=\frac{1}{\sqrt{N}}\sum_{m=0}^{N-1} x[m] \psi_{j...
...2}\psi[2^j m-k],
\;\;\;\;\mbox{(for all $k$ and all $j>j_0$)} \end{displaymath}](img175.png)
![\begin{displaymath}\begin{array}{l}
\varphi[m]=\sum_l h_{\varphi}[l]\sqrt{2} \v...
...
\psi[m]=\sum_l h_{\psi}[l]\sqrt{2} \varphi[2m-l] \end{array} \end{displaymath}](img177.png)
![$\displaystyle \frac{1}{\sqrt{N}}\sum_{m=0}^{N-1} x[m] 2^{j/2}\psi[2^j m-k]
=\fr...
...um_{m=0}^{N-1} x[m] 2^{j/2}
[\sum_n h_{\psi}[n-2k]\sqrt{2} \varphi[2^{j+1}m-n]]$](img190.png)
![$\displaystyle \sum_n h_{\psi}[n-2k][\frac{1}{\sqrt{N}}\sum_{m=0}^{N-1} x[m] 2^{(j+1)/2}
\varphi(2^{j+1}m-n)]$](img191.png)
![\begin{displaymath}
W_{\psi}[j+1,k]=\frac{1}{\sqrt{N}}\sum_{m=0}^{N-1}x[m]2^{(j+1)/2}\varphi(2^{j+1}m-n)
\end{displaymath}](img192.png)
![\begin{displaymath}\begin{array}{l}
W_{\psi}[j,k]=h_{\psi}[-n]*W_{\varphi}[j+1,...
...rphi}[-n]*W_{\varphi}[j+1,n]\vert _{n=2k,k\le 0}
\end{array} \end{displaymath}](img198.png)
![]() and
and ![]() from a given function
from a given function ![]() - can be implemented by
the analysis filter bank, the inverse wavelet transform - reconstructing the function
- can be implemented by
the analysis filter bank, the inverse wavelet transform - reconstructing the function
![]() from the coefficients
from the coefficients ![]() and
and ![]() - can be implemented by
the synthesis filter bank.
- can be implemented by
the synthesis filter bank.
