


Next: Wavelet Expansion
Up: wavelets
Previous: Scaling Functions
We denote by 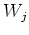 the difference between the function space
the difference between the function space 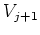 spanned
by scaling functions
spanned
by scaling functions
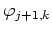 and the function
and the function 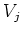 spanned by
spanned by
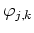 , i.e.
, i.e.
(where 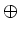 represents the union of the two spaces).
represents the union of the two spaces). 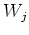 is composed of all
functions representable in
is composed of all
functions representable in 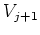 but not representable in
but not representable in 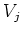 (as the scale
of the basis functions of
(as the scale
of the basis functions of 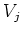 is too coarse for the details of these functions).
This can be carried out recursively to get:
is too coarse for the details of these functions).
This can be carried out recursively to get:
and finally:
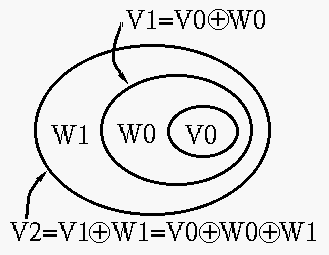
Similar to a function space 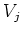 spanned by the scaling functions
spanned by the scaling functions
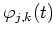 , the function space
, the function space 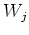 is also spanned by a set of basis
function, called the wavelet functions:
is also spanned by a set of basis
function, called the wavelet functions:
We see that the scaling sequence and the wavelet sequence correspond to
low-pass filter and band-pass filter, respectively.
Also, as the wavelet functions 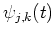 are members of the space
are members of the space 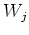 they span as well as all the super-spaces:
they span as well as all the super-spaces:
they can be expanded in the space 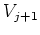 of next higher scale with doubled
resolution:
of next higher scale with doubled
resolution:
where 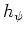 are the expansion coefficients. Usually we let
are the expansion coefficients. Usually we let 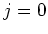 and drop
the subscripts
and drop
the subscripts 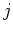 and
and 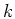 to indicate that any wavelet function
to indicate that any wavelet function 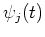 can be
expressed as a linear combination of the basis scaling functions
can be
expressed as a linear combination of the basis scaling functions
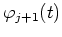 of the space with the next higher resolution:
of the space with the next higher resolution:
This is in the same form for the scaling functions:
It can be shown that the coefficients of the two expressions are related
Examples:
The Haar scaling function 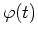 is a square pulse with unit height and
width, and the coefficients are
is a square pulse with unit height and
width, and the coefficients are
![$h_{\varphi}[0]=h_{\varphi}[1]=1/\sqrt{2}$](img109.png) . Now
the coefficients for the wavelet functions can be obtained as
. Now
the coefficients for the wavelet functions can be obtained as
and the wavelet function is:
where the two coefficients
![$h_{\psi}[0]=-h_{\psi}[0]=1/\sqrt{2}$](img112.png) are the second
row of the Haar matrix
are the second
row of the Haar matrix  .
.
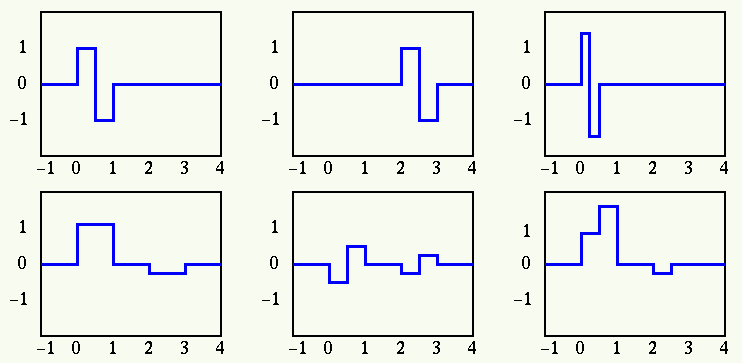
The first two panels show the wavelet functions of scale  :
:
 and
and
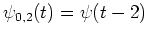 . Note
. Note
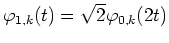 can be generated by the linear combination of
can be generated by the linear combination of
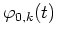 and
and 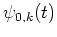 :
:
The 3rd panel shows the wavelet functions of scale 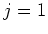 :
:
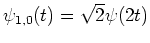 . The 4th panel shows a function in space
. The 4th panel shows a function in space  spanned by
spanned by
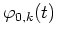 .
The 5th panel shows a function in space
.
The 5th panel shows a function in space 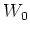 spanned by
spanned by 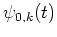 .
The 6th panel shows a function in space
.
The 6th panel shows a function in space
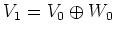 , a linear
combination of
, a linear
combination of
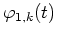 , or
, or
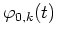 and
and 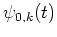 .
.



Next: Wavelet Expansion
Up: wavelets
Previous: Scaling Functions
Ruye Wang
2008-12-16
![]() the difference between the function space
the difference between the function space ![]() spanned
by scaling functions
spanned
by scaling functions
![]() and the function
and the function ![]() spanned by
spanned by
![]() , i.e.
, i.e.
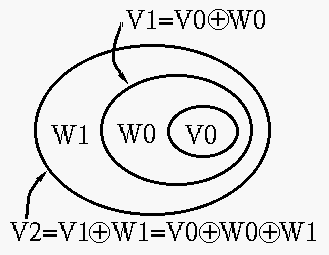
![]() spanned by the scaling functions
spanned by the scaling functions
![]() , the function space
, the function space ![]() is also spanned by a set of basis
function, called the wavelet functions:
is also spanned by a set of basis
function, called the wavelet functions:
![]() are members of the space
are members of the space ![]() they span as well as all the super-spaces:
they span as well as all the super-spaces:
![]() is a square pulse with unit height and
width, and the coefficients are
is a square pulse with unit height and
width, and the coefficients are
![]() . Now
the coefficients for the wavelet functions can be obtained as
. Now
the coefficients for the wavelet functions can be obtained as
![\begin{displaymath}\begin{array}{l} h_{\psi}[0]=(-1)^0 h_{\varphi}[1-l]=1/\sqrt{...
... h_{\psi}[1]=(-1)^1 h_{\varphi}[1-l]=-1/\sqrt{2}
\end{array} \end{displaymath}](img110.png)
![\begin{displaymath}\psi(t)=\sum_l h_{\psi}[l]\sqrt{2}\varphi[2t-l]
=\frac{1}{\s...
...-1 & 0.5 \le t < 1 0 & \mbox{otherwise} \end{array} \right. \end{displaymath}](img111.png)

![]() :
:
![]() and
and
![]() . Note
. Note
![]() can be generated by the linear combination of
can be generated by the linear combination of
![]() and
and ![]() :
:
![\begin{displaymath}\varphi_{1,k}(t)=\frac{\sqrt{2}}{2}[\varphi_{0,k}(t)+\psi_{0,k}(t)] \end{displaymath}](img118.png)