Scaling Functions

Consider a set of functions

$$\varphi_{j,k}(t)=2^{j/2}\varphi(2^j t-k)$$

where the specific function $\varphi(t)$ is to be determined later. These functions have two integer subscripts or parameters $j$ and $k$:

• The first subscript $j$ specifies the magnitude $2^{j/2}$ as well as the scale $2^j t$ of the function. A greater $j$ corresponds to a larger magnitude but a more compressed function (higher ``frequency'' representing more details). This corresponds to the parameter $n$ representing frequency in the basis functions $\varphi_n(t)=e^{-j2\pi nt}=cos(2\pi nt)-jsin(2\pi nt)$ for Fourier expansion. When $j\rightarrow -\infty$, $\varphi_{j,k}$ becomes infinitely wide (zero frequency) with infinitely small magnitude, while $j\rightarrow \infty$, $\varphi_{j,k}$ approaches a delta function with infinitely narrow width but infinitely high magnitude.
• The second subscript $k$ specifies the position (integer location, translation or shift) of the function. This does not have a counterpart in the basis functions for Fourier transform, where the position information is totally missing.

Replacing $j$ in the equation above by $j+1$, we get:

$$\varphi_{j+1,k}(t)=2^{(j+1)/2}\varphi(2^{j+1} t-k)=\sqrt{2} 2^{j/2}\varphi_{j,k}(2t-k)$$

indicating how a function $\varphi_{j+1,k}(t)$ at the $(j+1)th$ level is related to the corresponding function $\varphi_{j,k}(t)$ at the $jth$ level.

Corresponding to a specific index $j_0$, a subset of functions $\varphi_{j,k}\vert _{j=j_0}=\varphi_{j_0,k}$ spans a function space $V_{j_0}$. In general, there are many such functions spaces: $\cdots, V_{-1}, V_0, V_1, \cdots$.

If a family of functions $\varphi_{j,k}(t)$ satisfy the follow requirements, they become a set of basis functions that span a function space, so that a given function $x(t)$ can be represented as a linear combination of these bases:

$$x(t)=\sum_j \sum_k c_{j,k} \varphi_{j,k}(t)$$

• The functions $\varphi_{j,k}(t)$ have to be orthogonal to its integer translates:
  
  $$(\varphi_{j,k}(t),\varphi_{j,l}(t))=\int \varphi_{j,k}(t)\;\varphi_{j,l}(t))dt =0\;\;\;\;\;\mbox{if $l\ne k$}$$
  
  

• The function space $V_j$ spanned by a set of functions $\varphi_{j,k}$ is a subspace of the function space $V_{j+1}$ spanned by the functions of a higher scale $\varphi_{j+1,k}$ (with double-resolution and capable of representing more details):
  
  $$V_{-\infty} \subset \cdots, \subset V_{-1} \subset V_0 \subset V_1,\cdots, \subset V_{\infty}$$
  
  

• The only function contained in all subspaces $V_j,\;(\cdots,-1,0,1,\cdots)$ is $x(t)=0$ (constant of lowest resolution or frequency carrying no information), which is the only function contained in $V_{-\infty}$, i.e., $V_{-\infty}=\{x(t)=0\}$.

• A function can be represented with arbitrary precision by including terms $\varphi_{j,k}$ of progressively higher scales (greater $j$) for representing more details (high frequency components) of the function. Any square-integrable functions (with arbitrary details) can be represented in $V_{\infty}$, i.e.,
  
  $$V_{\infty}=L^2(R)$$
  
  
  where $L^2(R)$ represents all square-integrable functions $x(t)$ ( $\int f^2(t) dt <\infty$).

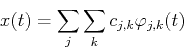
Functions satisfying these requirements are called scaling functions. As the basis functions, a subset of scaling functions $\varphi_{j,k}$ with a certain scale $j$ can only represent a function $x(t)$ up to a certain level of details corresponding to the scale of the bases. All details in $x(t)$ finer than the limit of the scales of $\varphi_{j,k}$ are lost. However, such details can be better represented by the basis functions of the next higher scale $\varphi_{j+1,k}$. In general, space $V_{j+1}$ contains all functions representable in $V_j$, as well as those functions with more details not representable in $V_j$, i.e., $V_j \subset V_{j+1}$, and a function can always be more precisely represented by increasing the scales (the parameter $j$) of the bases.

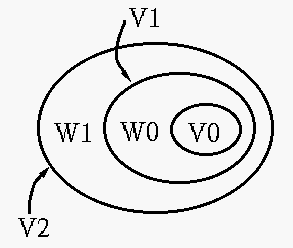
Note: The nested relations between the sequence of subspaces shown above is closely related to the Gaussian-Laplacian pyramid discussed earlier. Essentially they both state that a signal can be decomposed into a set of components each representing details of different levels contained in the signal. The images in the Laplacian pyramid correspond to the subspaces $W_j$ as they both represent the difference between two consecutive levels of details.

The basis functions $\varphi_{j,k}(t)$ are themselves members of the space $V_j$ they span as well as all the super-spaces:

$$\varphi_{j,k}(t) \in V_j \subset V_{j+1} \subset \cdots$$

And they can be expanded in the space $V_{j+1}$ of next higher scale with doubled resolution:

$$\varphi_{j,k}(t) =\sum_l h_{\varphi}[l] \varphi_{j+1,l}(t) =\sum_l h_{\varphi}[l] 2^{(j+1)/2} \varphi(2^{j+1}t-l)$$

where $h_{\varphi}$ are called scaling functions coefficients. Usually we let $j=0$ and drop the subscripts $j$ and $k$ to indicate that any scaling function $\varphi_j(t)$ can be expressed as a linear combination of the basis scaling functions $\varphi_{j+1,k}(t)$ of the space with the next higher resolution:

$$\varphi(t)=\sum_l h_{\varphi}[l]\sqrt{2} \varphi(2t-l)$$

This is called refinement, dilation or MRA (multiresolution analysis) equation.

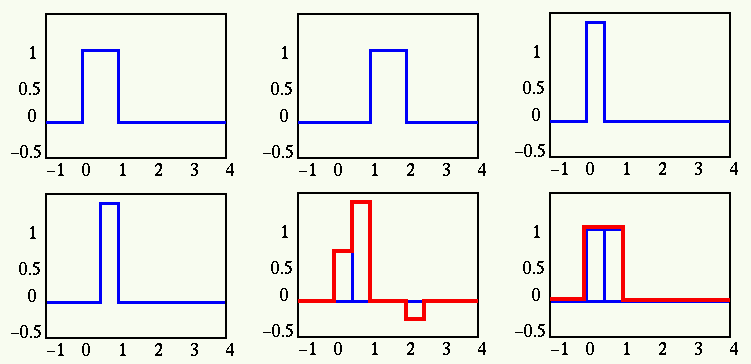
The first 4 panels show the scaling functions: $\varphi(t)=\varphi_{0,0}(t)$, $\varphi_{0,1}(t)=\varphi(t-1)$, $\varphi_{1,0}(t)=\sqrt{2}\varphi(2t)$, and $\varphi_{1,1}(t)=\sqrt{2}\varphi(2t-1)$, The 5th panel shows a function in space $V_1$ spanned by $\varphi_{1,k}(t)$. The 6th panel shows $\varphi_{0,0}(t)$ as a special function in space $V_1$.

Example: The Haar scaling function at level $j=0$ is defined as a square pulse of unit width and unit height:

$$\varphi(t)=\varphi_{0,0}(t)=\left\{ \begin{array}{ll}1 & 0\le t < 1 \\ 0 & \mbox{otherwise} \end{array} \right.$$

Scaling function $\varphi(t)$ together with its shifted versions $\varphi_{0,k}(t)=\varphi(t-k),\;(k>0)$ form a set of basis functions that span the space $V_0$. The scaling functions of higher scales ($j>0$) for higher resolutions (for signal details) can be obtained by

$$\varphi_{j,k}(t)=2^{j/2}\varphi(2^j t-k)$$

For example, when $j=1$, we have

$$\varphi_{1,k}(t)=\sqrt{2}\varphi(2t-k)$$

A given function $x(t)$ can be expanded as a linear combination of these scaling (basis) functions:

$$x(t)=0.5\varphi_{1,0}(t)+\varphi_{1,1}(t)-0.25\varphi_{1,4}(t)$$

This is shown in panel 5 of the figure above.

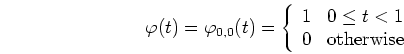
Moreover, the Haar scaling functions in space $V_0$ are also functions in space $V_1$ and they can be expressed as a linear combination of the basis functions $\varphi_{1,k}(t)$:

$$\varphi_{0,k}(t)=\frac{1}{\sqrt{2}}\varphi_{1,2k}(t) +\frac{1}{\sqrt{2}}\varphi_{1,2k+1}(t)$$

This is shown in panel 6 of the figure above. In particular,

$$\varphi_{0,0}(t)=\frac{1}{\sqrt{2}}\varphi_{1,0}(t)+\frac{1}{\sqrt{2}}\varphi_{1,1}(t)$$

But as

$$\varphi_{1,0}(t)=\sqrt{2}\varphi_{0,0}(2t),\;\;\;\; \varphi_{1,1}(t)=\sqrt{2}\varphi_{0,0}(2t-1)$$

the above can be written as

$$\varphi(t)=\varphi_{0,0}(t)=h_{\varphi}[0]\sqrt{2}\varphi_{0,... ...0,0}(2t-1) =\sum_{l=0}^1 h_{\varphi}[l] \sqrt{2}\varphi(2t-l)$$

where the two coefficients $h_{\varphi}[0]=h_{\varphi}[0]=1/\sqrt{2}$ are the first row of the Haar matrix ${\bf H}_2$.