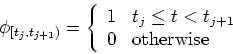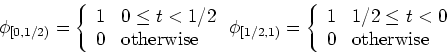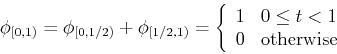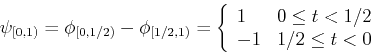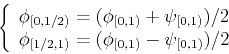next up previous
Next: Scaling Functions Up: wavelets Previous: Why Wavelet?

Haar Wavelets

A continuous signal can be approximated by a sequence of unit impulse functions, also called scaling functions, weighted by the sampling values of the intensity or amplitude of the signal:

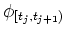\begin{displaymath}x(t)=\sum_i s_i \phi_{[t_j,t_{j+1})} \end{displaymath}

where $\phi_{[t_j,t_{j+1})}$ is a unit impulse with width 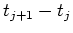$t_{j+1}-t_j$ defined as

\begin{displaymath}\phi_{[t_j,t_{j+1})}=\left\{ \begin{array}{ll} 1 & t_j \le t < t_{j+1} 0 & \mbox{otherwise} \end{array} \right. \end{displaymath}

Consider two adjacent impulse functions:

\begin{displaymath}\phi_{[0,1/2)}=\left\{ \begin{array}{ll} 1 & 0 \le t <1/2 \\... ... 1 & 1/2 \le t <0 0 & \mbox{otherwise} \end{array} \right. \end{displaymath}

The sum of two adjacent impulse functions is a wider impulse:

\begin{displaymath}\phi_{[0,1)}=\phi_{[0,1/2)}+\phi_{[1/2,1)}=\left\{ \begin{arr... ...} 1 & 0 \le t < 1 0 & \mbox{otherwise} \end{array} \right. \end{displaymath}

and the difference of two adjacent impulse functions is the basic wavelet, denoted by

\begin{displaymath}\psi_{[0,1)}=\phi_{[0,1/2)}-\phi_{[1/2,1)}=\left\{ \begin{arr... ...l} 1 & 0 \le t < 1/2 -1 & 1/2 \le t <0 \end{array} \right. \end{displaymath}

By solving (adding and subtracting) the two equations above, the two impulse functions can be obtained:

\begin{displaymath}\left\{ \begin{array}{l} \phi_{[0,1/2)}=(\phi_{[0,1)}+\psi_... ...hi_{[1/2,1)}=(\phi_{[0,1)}-\psi_{[0,1)})/2 \end{array} \right. \end{displaymath}

Then any two-sample function can be written as

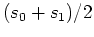\begin{displaymath}x(t)=s_0 \phi_{[0,1/2)} + s_1 \phi_{[1/2,1)} =s_0 \frac{\phi... ...=\frac{s_0+s_1}{2} \phi_{[0,1)}+\frac{s_0-s_1}{2} \psi_{[0,1)} \end{displaymath}

where $(s_0+s_1)/2$ represents the average of the function and 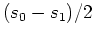$(s_0-s_1)/2$ represents the change in the function. This is the Haar transform of the function. See here for more details.


Ruye Wang 2008-12-16