Why Wavelet?

A time signal $x(t)$ contains complete information in time domain, i.e., the amplitude of the signal at any given moment $t$. However, no information is explicitly available in $x(t)$ regarding the frequency contents of the signal. On the other hand, as the spectrum $X(f)$ obtained by Fourier transform of the time signal $x(t)$ is extracted from the entire time duration of the signal, it contains complete information in the frequency domain in terms of the magnitude and phase angle of any frequency component $f$, but there is no information explicitly available in the spectrum regarding the temporal characteriscs of the signal such as where in time certain frequency component appeared. Neither $x(t)$ in time domain nor $X(f)$ in frequency domain provides complete description of the signal.

To address this dilemma, we can truncate the signal $x(t)$ by a time window $w(t-\tau)$

$$x'(t)=w(t-\tau) x(t)$$

where the time window has width $T$ and can shift in time according to $\tau$:

$$w(t)=\left\{\begin{array}{ll}1 & 0<t<T 0 & \mbox{otherwise} \end{array} \right.$$

The spectrum of this windowed signal is for the specific time period $T$ only. One immediate drawback of this windowed signal is the severe distortion in frequency domain caused by the sudden truncation in time domain. To reduce this distortion, the square time window can be replaced by a smooth Gaussian bell-shaped window with gradual decay:

$$x'(t)=g(t) x(t),\;\;\;\;\mbox{where}\;\;\; g(t)=c\;exp((t-\tau)^2/\sigma^2)$$

The Fourier transform of this Gassian filtered time signal is called the Gabor transform. Although the spectral property of a windowed signal can be better localized in time, its resolution in frequency is reduced as its spectrum is blurred by the convolution with $G(f)={\cal F}[g(t)]$:

$$X'(f) = X(f)*G(f)$$

Alternatively, we can assume the truncated signal $x(t)$ repeats itself outside a finite period T. In this case, the spectrum becomes discrete, composed of a set of infinite number of frequency components $X[k]$ ( $k=0,\pm 1, \pm 2, \cdots$) for discrete frequencies $f=k f_0=k/T$, including DC component $X[0]$ at $f=0$, fundamental frequency $X[1]$ at $f_0=1/T$, and the higher harmonics $X[k]$ ($k>1$). In this discrete spectrum, the information of any frequency in the gap between any two consecutive frequency components $X[k]$ and $X[k+1]$ is lost. Moreover, the higher temporal resolution we achieve by reducing $T$, the lower frequency resolution will result due to the larger gaps $f_0=1/T$ between frequency components.

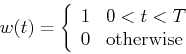
We see that it is simply impossible to have the complete information of a given signal in both time and frequency domains at the same time, as increasing the resolution in one domain will necessarily reduce that in the other. This effect is referred to as Heisenberg uncertainty, as it is anologous to the fact in quantum physics that the position and momentum of a particle cannot be measured simultaneously, higher precision in one quantity implies lower in the other.

If the characteristics of the signal in question do not change much over time, i.e, the signal is stationary, then Fourier transform is sufficient for the analysis of the signal. However, in many applications it is the transitory or nonstationary aspects of the signal (e.g., drift, trends, abrupt changes) that are of most interest. In such cases, Fourier analysis is unable to detect when/where such events take place and is therefore not suitable to describe or represent them.

In order to overcome this limitation of Fourier analysis to gain information in both time and frequency domain, a different kind of transform, called wavelet transform can be used. Wavelewt transform can be viewed as a trade-off between time and frequency domains. Unlike Fourier transform which transforms a signal between time (or space) and frequency domains, wavelet transform emphasizes locations and scales (instead of frequency). From the lowest time scale to the highest, the scale is always halved to reveal more details (time resolution doubled), while the gap between consecutive scales is doubled, i.e., the scale resolution is reduced as illustrated by the Heisenberg Box (Cell) below: