Metropolis-Hastings sampling

The goal of the M-H algorithm is to design a Markov chain so that its stationary distribution is the same as the desired distribution $p(X)$, i.e., after the ``burn-in'' peroid of some $m$ iterations, the consecutive states $X_t$ $(t>m)$ of the chain are statistically equivalent to samples drawn from $p(X)$.

M-H sampling assumes an arbitrary proposal distribution $q(.\vert X)$ that depends on the current state $X$ of the Markov chain. For example, a multivariate normal distribution with a mean vector same as $X$ and some covariance matrix. A candidate state $Y$ generated by the proposal distribution is accepted with the probability:

$$\alpha(X_t,Y)=min(1, \frac{p(Y)q(X_t\vert Y)}{p(X_t)q(Y\vert X_t)})$$

If the candidate $Y$ is accepted, then next state is $X_{t+1}=Y$, otherwise if $Y$ is rejected, the next state remains the same as the previous state $X_{t+1}=X_t$. The ratio can be written as

$$\frac{p(Y)q(X_t\vert Y)}{p(X_t)q(Y\vert X_t)}=\frac{p(Y)/q(Y\... ...)} =\frac{\mbox{importance of $Y$}}{\mbox{importance of $X$}}$$

i.e., if $Y$ is more important than $X$, it is accepted as the next step, but if $Y$ is less important, it is rejected.

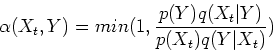
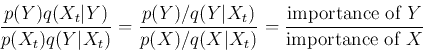
  Initialize X_0, set t=0.
  Repeat {
    get a sample point Y from q(.|X_t)
    get a sampel value u from a Uniform(0,1)
    if u < \alpha(X_t, Y) then X_{t+1}=Y (Y accepted)
    else X_{t+1}=X_t (Y rejected)
    t=t+1
  }

Proof of M-H algorithm

Now we show that the states of the Markov chain generated by the M-H algorithm do satisfy the requirement. First we denote the probability of the transition from a given state $X$ to the next $Y$ by

$$Prof(X \rightarrow Y)\stackrel{\triangle}{=}P(Y\vert X)=q(Y\vert X)\alpha(X,Y)$$

where $q(Y\vert X)$ is the probability that $Y$ is generated with current state $X$, and $\alpha(X,Y)$ is the probability that $Y$ is accepted as the next state, following current state $X$.

Step 1: First we show that the detailed balance equation defined below always holds:

$$P(Y\vert X)p(X)=P(X\vert Y)p(Y), \mbox{ i.e., } q(Y\vert X) \alpha(X,Y)p(X)=q(X\vert Y) \alpha(Y,X)p(Y)$$

Consider the following three exhaustive cases:

• Case 1: $p(Y)q(X\vert Y)=p(X)q(Y\vert X)$, then $\alpha(X,Y)=\alpha(Y,X)=1$, and
  
  $$P(Y\vert X)p(X)=q(Y\vert X)p(X) \alpha(X,Y)=q(Y\vert X)p(X)=P... ...vert Y)p(Y)=q(X\vert Y)p(Y) \alpha(Y,X)=q(X\vert Y)p(Y)=P(X,Y)$$
  
  
  i.e.,
  
  $$P(Y\vert X)p(X)=P(X\vert Y)p(Y)$$
  
  

• Case 2: $p(Y)q(X\vert Y)>p(X)q(Y\vert X)$, then
  
  $$\alpha(X,Y)=\frac{p(Y)q(X\vert Y)}{p(X)q(Y\vert X)},\;\;\;\alpha(Y,X)=1$$
  
  
  Hence
  

  $$P(Y\vert X)p(X) = q(Y\vert X)\alpha(X,Y)p(X)=q(Y\vert X)\frac{p(Y)q(X\vert Y)}{p(X)q(Y\vert X)}p(X)$$

  $$= q(X\vert Y)p(Y)=q(X\vert Y)\alpha(Y,X)p(Y)=P(X\vert Y)p(y)$$

  
  

• Case 3: $p(Y)q(Y\vert\vert X)>p(Y)q(X\vert Y)$, then
  
  $$\alpha(Y,X)=\frac{p(X)q(Y\vert X)}{p(Y)q(X\vert Y)},\;\;\;\alpha(X,Y)=1$$
  
  
  By similar argument in case 2, we get
  
  $$P(X\vert Y)p(Y)=P(Y\vert X)p(X)$$
  
  

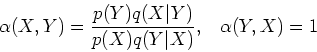
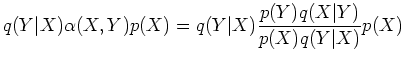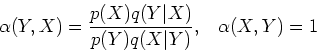
Step 2: Next we show that if $X_t$ is from $p(X)$, then $X_{t+1}$ generated by M-H method will also be from the same $p(X)$. Rewrite the balance equation as

$$P(X_{t+1}\vert X_t)p(X_t)=P(X_t\vert X_{t+1})p(X_{t+1})$$

and integrate both sides respect to $X_t$ to get

$$\int P(X_{t+1}\vert X_t)p(X_t dX_{t})=\int P(X_t\vert X_{t+1})p(X_{t+1}) dX_t=p(X_{t+1})$$

The left-hand side gives the marginal distribution of $X_{t+1}$ under the assumption that $X_t$ is from $p(X)$, and the right-hand side shows $X_{t+1}$ will also be from the same distribution $p$.