


Next: Metropolis-Hastings sampling
Up: MCMC
Previous: Statistical Sampling
Monte Carlo methods can solve these general problems:
- draw random variables from a probability density function
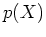 where
where
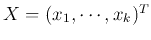 is a k-dimensional random vector.
is a k-dimensional random vector.
- estimate integral
Monte Carlo methods can be used to evaluate the integrations for
![$E[f(X)]$](img67.png) in Baysian inference, by drawing samples
in Baysian inference, by drawing samples
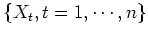 from
from 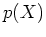 and then approximating
and then approximating
This is referred to as Monte Carlo integration.
A Markov Chain is a sequence of random variables
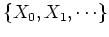 generated by a Markov process. At each time
generated by a Markov process. At each time 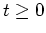 , the next state
, the next state
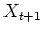 is sampled from a distribution called transition kernel
is sampled from a distribution called transition kernel
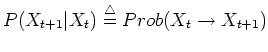 .
By definition, the next state
.
By definition, the next state 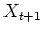 of a Markov process only depends
on the current state
of a Markov process only depends
on the current state 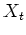 , but is independent of all previous states
, but is independent of all previous states
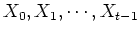 (limited horizon):
(limited horizon):
Let
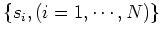 be the
be the 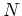 possible states of the
Markov chain. We define
possible states of the
Markov chain. We define
Then the following Chapman-Kolomogrov equation gives the
probability of the next state taking a specific value 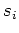 :
:
We represent both distributions at stage 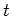 and
and 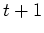 column vectors:
column vectors:
then the Chapman-Kolomogrov equation can be expressed in matrix
form:
This state transition can be recursively extended until reaching the
initial state 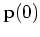 :
:
If the Markov chain is irreducible and aperiodic, the distribution
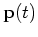 may reach a stationary distribution
may reach a stationary distribution 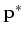 after a large number of transitions, independent of the initial
distribution
after a large number of transitions, independent of the initial
distribution 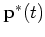 . Any further transition will not change
the distribution any more:
. Any further transition will not change
the distribution any more:
In other words, the stationary distribution 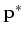 is the
eigenvector of the transition matrix
is the
eigenvector of the transition matrix 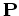 corresonding to the
eigenvalue
corresonding to the
eigenvalue 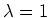 .
.
A sufficient condition for a unique stationary distribution is
that the detailed balance equation holds:
under this condition the chain is reversible, and the ith element of
vector
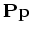 is
is
(last equal sign due to
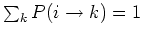 ), i.e.,
), i.e.,
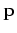 is stationary. This condition guarantees stationary
distribution from the beginning of the chain, and is not a necessary
condition as the chain can also become stationary gradually.
is stationary. This condition guarantees stationary
distribution from the beginning of the chain, and is not a necessary
condition as the chain can also become stationary gradually.
As an example, assume the transition matrix of a 3-state Markov chain is:
then the stable distribution 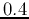 ,
, 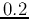 and
and 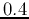 will be reached
after a few iterations, independent of the initial distribution
will be reached
after a few iterations, independent of the initial distribution 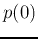 .
.



Next: Metropolis-Hastings sampling
Up: MCMC
Previous: Statistical Sampling
Ruye Wang
2018-03-26
![\begin{displaymath}E[f(X)]\approx \frac{1}{n}\sum_{t=1}^n f(X_t) \end{displaymath}](img69.png)
![]() generated by a Markov process. At each time
generated by a Markov process. At each time ![]() , the next state
, the next state
![]() is sampled from a distribution called transition kernel
is sampled from a distribution called transition kernel
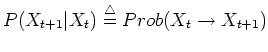 .
By definition, the next state
.
By definition, the next state ![]() of a Markov process only depends
on the current state
of a Markov process only depends
on the current state ![]() , but is independent of all previous states
, but is independent of all previous states
![]() (limited horizon):
(limited horizon):
![]() be the
be the ![]() possible states of the
Markov chain. We define
possible states of the
Markov chain. We define
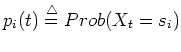 as the ith component
of the
as the ith component
of the 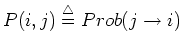 as the
component in the ith row, jth column of the
as the
component in the ith row, jth column of the 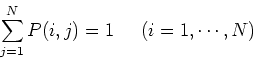
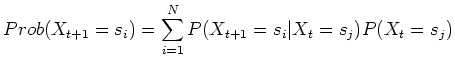
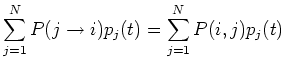
![]() may reach a stationary distribution
may reach a stationary distribution ![]() after a large number of transitions, independent of the initial
distribution
after a large number of transitions, independent of the initial
distribution ![]() . Any further transition will not change
the distribution any more:
. Any further transition will not change
the distribution any more:
![\begin{displaymath}{\bf P}=\left[ \begin{array}{lll}
0.5 & 0.5 & 0.25 \\
0.25 & 0.0 & 0.25 \\
0.25 & 0.5 & 0.5 \end{array} \right]
\end{displaymath}](img110.png)