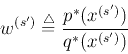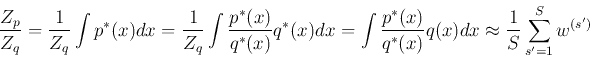Statistical Sampling

Next: Markov Chain Monte Carlo Up: MCMC Previous: Bayesian Inference

Statistical Sampling

The average height of all people in Cambridge can be obtained by measuring the heights of all people in Cambridge and then averaging them:

$\begin{displaymath}E_{p\in C} [h(p)] =\frac{1}{\vert C\vert} \sum_{p\in C} h(p) \end{displaymath}$

Alternatively, this can be approximated by sampling the population:

$\begin{displaymath}E_{p\in C} [h(p)] \approx \frac{1}{S} \sum_{s=1}^S h(p^{(s)}) \end{displaymath}$

where $\{ p^{(s)}\vert s=1,\cdots,S) \} \in C$ is a subset of all people in Cambridge

.

Similarly, the following expectation can be approximated by

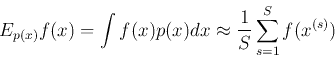
$\begin{displaymath}E_{p(x)} f(x)=\int f(x) p(x) dx \approx \frac{1}{S} \sum_{s=1}^S f(x^{(s)}) \end{displaymath}$

where $x^{(s)}$ are drawn from the distribution

. This is called simple Monte Carlo method. But how to sample a given distribution

?

Direct sampling
We can sample from directly. First find the accumlative density of :

$\begin{displaymath}F(x)=\int_{-\infty}^x p(x')dx' \end{displaymath}$

whose value will range from 0 ( $x\rightarrow -\infty$ ) to 1 ( $x\rightarrow \infty$ ). We then sample $u \sim Uniform[0,1]$ (corresponding to $-\infty <x< \infty$ ) and map back to : $x(u)=F^{-1}(u)$ . This is not applicable if the true is not normalized, i.e., we only have the unnormalized density without the normalizing factor $Z_x=\int p^*(x)dx$ .
Rejection (acceptance) sampling
Assume we want to sample a complicated distribution which is not normalized, i.e., the normalizing factor $Z_p=\int p^*(x)dx$ (not necessarily equal to 1) is unknown.The rejection sampling method makes use of a simpler proposal distribution , also not normalized with unknown $Z_q=\int q^*(x)dx$ . Assume a scalar can be obtained so that is the upper bound of for all range of :

$\begin{displaymath}cq^*(x) > p^*(x)\;\;\;\;\;\mbox{for all $x$} \end{displaymath}$

We then draw two random numbers $u\sim Uniform[0,cq^*(x)]$ and $x\sim q(x)$ . This is accepted as a sample from if or rejected if otherwise. As a special case, could be a uniform distribution with constant values over .
The accepted represent the desired distribution , because the rate of acceptance is proportional to the height of . Rejection sampling works best if the proposal distribution is similar to the actual distribution , as otherwise many values will be rejected.
Importance sampling
Importance sampling is not a method for generating samples from , instead it is used to estimate the expectation of a function . Importance sampling can avoid the rejection (therefore wasted effort) in previous method. To find the following expectation of with respect to a complicated distribution with unknow scalar :

$\begin{displaymath}E_{p(x)}[f(x)]=\int f(x) p(x) dx \end{displaymath}$

we can sample a simpler proposal distribution to approximate the expectation:

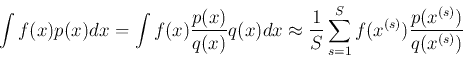
$\begin{displaymath}\int f(x) p(x) dx =\int f(x) \frac{p(x)}{q(x)} q(x) dx \appr... ...frac{1}{S}\sum_{s=1}^S f(x^{(s)})\frac{p(x^{(s)})}{q(x^{(s)})} \end{displaymath}$

where the samples $x^{(s)}$ are drawn from .
If the normalizing scalars $Z_p=\int p^*(x)dx$ and $Z_q=\int q^*(x)dx$ are unknown, the above can still be obtained by

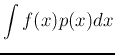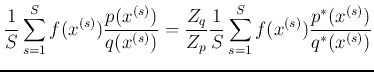$\displaystyle \int f(x) p(x) dx$ $\textstyle \approx$ $\displaystyle \frac{1}{S}\sum_{s=1}^S f(x^{(s)})\frac{p(x^{(s)})}{q(x^{(s)})} =\frac{Z_q}{Z_p}\frac{1}{S}\sum_{s=1}^S f(x^{(s)})\frac{p^*(x^{(s)})}{q^*(x^{(s)})}$

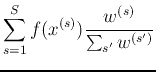$\textstyle \approx$ $\displaystyle \sum_{s=1}^S f(x^{(s)})\frac{w^{(s)}}{\sum_{s'} w^{(s')}}$

where $w^{(s')}$ is the weight for sample defined as

$\begin{displaymath}w^{(s')} \stackrel{\triangle}{=}\frac{p^*(x^{(s')})}{q^*(x^{(s')})} \end{displaymath}$

The last step is due to the following:

$\begin{displaymath}\frac{Z_p}{Z_q}=\frac{1}{Z_q} \int p^*(x)dx =\frac{1}{Z_q} \i... ...p^*(x)}{q^*(x)}q(x)dx\approx \frac{1}{S}\sum_{s'=1}^S w^{(s')} \end{displaymath}$

Importance sampling approximates the expectation of by a weighted average of the function evaluated at samples $x^{(s)}$ taken from , instead of . The function of the weights $w^{(s)}$ is to compensate for sampling the wrong distribution. When $p(x^{(s)})>q(x^{(s)})$ , $w^{(s)}>1$ will increase the importance of the sample $x^{(s)}$ where $p(x^{(s)})$ is under-sampled, but when $p(x^{(s)})<q(x^{(s)})$ , $w^{(s)}<1$ will derease the importance of the sample $x^{(s)}$ where $p(x^{(s)})$ is over-sampled.

Importance sampling and rejection sampling work well only if the proposal density

is similar to

, which may be difficult in practice.

Next: Markov Chain Monte Carlo Up: MCMC Previous: Bayesian Inference

Ruye Wang 2018-03-26